Viktiga aspekter
- ADC-enheter används flitigt för att omvandla analoga signaler, som ljud och ljus, till digitala värden, vilket möjliggör användning i en mängd olika applikationer.
- Samplingsfrekvensen hos en ADC anger hur många avläsningar som görs varje sekund, och en högre samplingsfrekvens leder till en mer exakt representation av signalen.
- Bithastigheten för en ADC påverkar kvaliteten på den erhållna datan, där fler bitar resulterar i mjukare och noggrannare mätningar. Det finns olika typer av ADC som erbjuder olika fördelar vad gäller hastighet, precision och energiförbrukning.
Analog-till-digital-omvandlare (ADC) är avgörande för att överföra verkliga händelser till data som kan användas i programmeringssammanhang. Men hur kan en ADC omvandla analoga signaler till digitala data som vi kan använda överallt?
Användningsområden för ADC
ADC-enheter är vanliga i många elektroniska system. De finns i mobiltelefoner för att omvandla röst till binär data, i bilar för att mäta hjulens rotation och i oscilloskop för att fånga och visa signaler. De är särskilt viktiga i video- och ljudteknik, där det är nödvändigt att konvertera ljus och ljud till digital information.
Vad är samplingsfrekvens och hur påverkar den en ADC?
En nyckelparameter för en ADC är samplingsfrekvensen, det vill säga antalet avläsningar som görs varje sekund.
Avancerade oscilloskop kan göra tiotusentals avläsningar per sekund, medan enklare ADC-enheter som MCP3008 kan göra runt tvåhundratusen. I ljudsammanhang är en samplingsfrekvens på 44 100 per sekund (44,1 kHz) vanligt förekommande.
Ju fler avläsningar som görs, desto mer exakt kan en signal återskapas. I vissa tillfällen är detta avgörande, medan det i andra fall kan vara mindre viktigt. Om vi exempelvis bygger en faderbank för att kontrollera elektronik, som de som används i ljus- eller ljudmixerbord, är det osannolikt att värdena vi behöver mäta kommer att förändras snabbt eftersom våra fingrar inte kan röra sig så snabbt. Då räcker det med att ta tillräckligt med avläsningar för att resultatet ska kännas smidigt och responsivt.
Vad är bithastighet och hur påverkar den kvaliteten på en ADC?
Kvaliteten på den avläsning vi får är också viktig. Detta bestäms i stor utsträckning av bithastigheten, som anger hur många olika nivåer vi kan använda för att digitalt representera spänningen. Fler bitar innebär att vi kan registrera fler potentiella värden i varje avläsning, vilket resulterar i ett mjukare och mer exakt slutresultat.
Vi har tidigare diskuterat hur binära tal fungerar, och det kan vara en bra startpunkt om du är osäker. Men hur många bitar behöver vi egentligen? Återigen, det beror på vad vi ska åstadkomma. Ibland kan vi vara begränsade av det protokoll vi använder. Till exempel är MIDI 1.0-protokollet begränsat till sju-bitars (och ibland fjorton-bitars) värden. I andra fall kan den begränsande faktorn vara den mänskliga perceptionen. Om en ökad detaljrikedom inte ger någon märkbar förbättring av resultatet, kanske det inte är värt besväret.
Hur förbättrar multiplexering ADC-kvaliteten?
Populära ADC-kretsar som ADS1115 och MCP3008 erbjuder många ingångar. Men de innehåller i grunden bara en enda ADC. Detta är möjligt tack vare de inbyggda multiplexerna i dessa enheter. Multiplexer finns överallt inom elektronik och telekommunikation. De är digitala omkopplare som fungerar som en trafikledare för din ADC. ADC:n kan läsa av en kanal, sedan nästa och så vidare. Så om du har åtta kanaler och en samplingsfrekvens på 200 000 kan du gå igenom dem alla och ta 25 000 samplingar per kanal.
Vilka typer av ADC finns det?
ADC-enheter fungerar på olika sätt, beroende på de krav som ställs på kostnad och prestanda.
En Flash ADC fungerar genom en komplicerad spänningsdelare. Ett motståndsnätverk delar upp referensspänningen i flera steg, som sedan jämförs med ingången med hjälp av komparatorer. Flash ADC:er är extremt snabba, men deras bitdjup begränsas av antalet komparatorer som krävs. De är även relativt energikrävande av samma anledning.
En subranging ADC försöker lösa dessa problem genom att dela upp arbetet mellan två separata enheter: en för att grovt uppskatta spänningen och en andra för att göra en exakt mätning. Genom att dela upp arbetet kan antalet komparatorer minskas. Vissa subranging ADC:er delar upp processen i tre steg, med inbyggd felkorrigering.
SAR (Successive Approximation Register) ADC:er arbetar genom en sorts binär sökning. Om vi till exempel har åtta bitar att fylla, börjar SAR med 10000000, vilket är mittvärdet (00000000 är det lägsta och 11111111 är det högsta). Om spänningen är högre än denna mittpunkt, behåller SAR den mest signifikanta biten som 1; om inte, ändrar SAR den till 0. Vi kan sedan upprepa processen för nästa bit, och så vidare. Detta kommer successivt att närma det gissade värdet till det faktiska värdet:
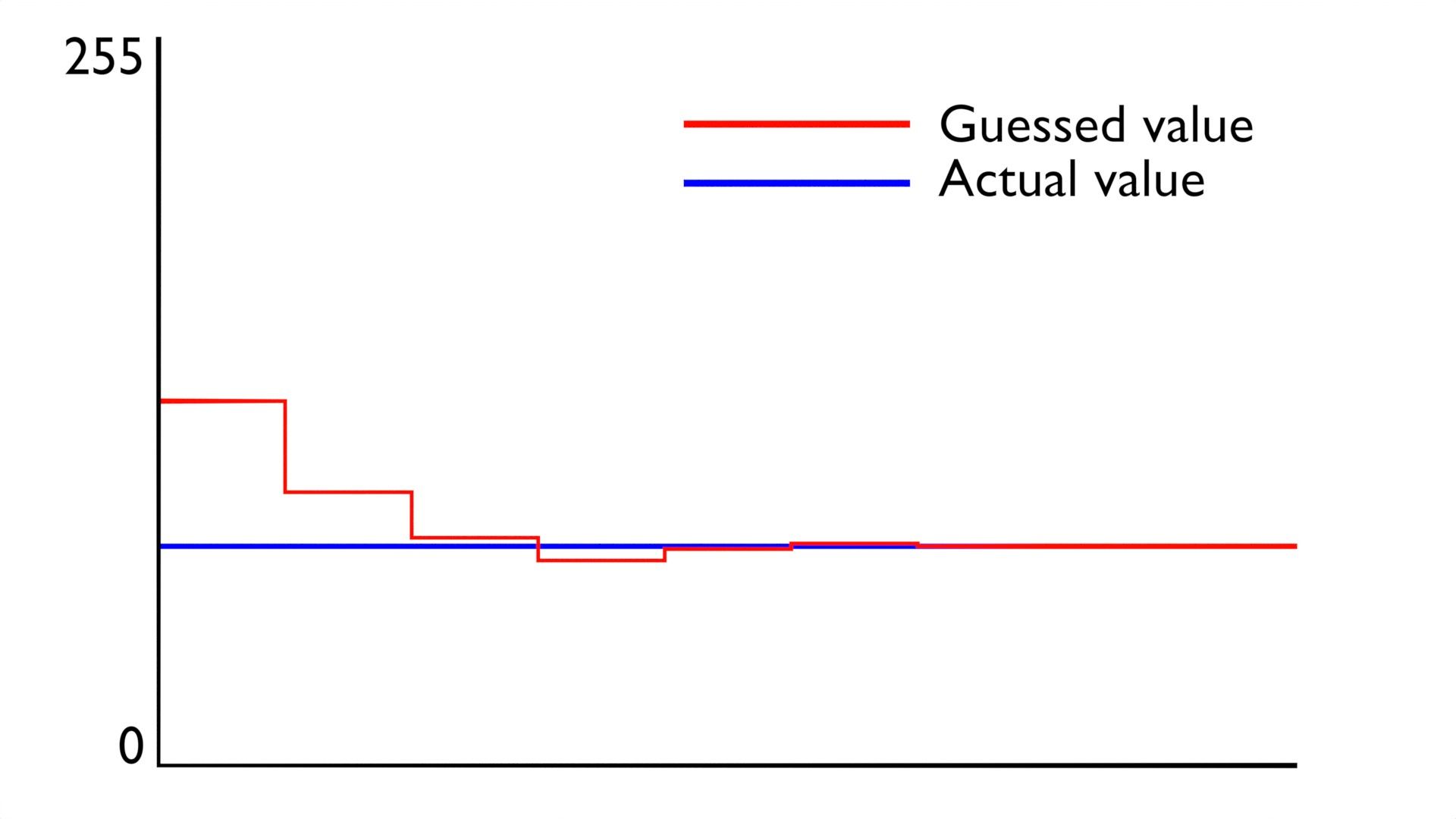
På detta sätt begränsar vi sökningen kontinuerligt, halverar möjligheterna och frågar om resultatet är högre eller lägre än mittpunkten. I detta fall ligger värdet någonstans mellan 0 och 255; efter några iterationer har ADC räknat ut att det är omkring 77.
Sigma-delta-omvandlare är nog de svåraste att förstå. De används för musikaliska och signalmätande applikationer med hög precision. De fungerar genom att översampla en signal och finjustera resultatet genom avancerad filtrering och matematik. Denna process minskar samplingsfrekvensen samtidigt som precisionen ökar. Dessa ADC:er är bra när brus och precision är viktigare än hastighet.
Slutligen finns det integrerande ADC:er, som är ännu långsammare än sigma-delta. De fungerar med hjälp av en kondensator, där laddningshastigheten kan användas för att avgöra ingångsspänningen. Samplingsfrekvensen är ofta synkroniserad med strömförsörjningsfrekvensen, vilket hjälper till att minimera brus.
Vad är Nyquist-Shannon teorin?
Låt oss anta att vi vill beskriva en analog signal digitalt. För att göra detta behöver vi minst två punkter för varje given cykel: en på toppen och en på botten. Därför måste vår samplingsfrekvens vara minst två gånger den högsta frekvens vi förväntar oss att mäta.
Detta kallas Nyquist-frekvensen, efter den svensk-amerikanske fysikern Harry Nyquist. Teorin är namngiven efter Nyquist och Claude Shannon (en framstående matematiker och kryptograf) men inte efter Edmund Whittaker, som kom på idén innan någon av dem.
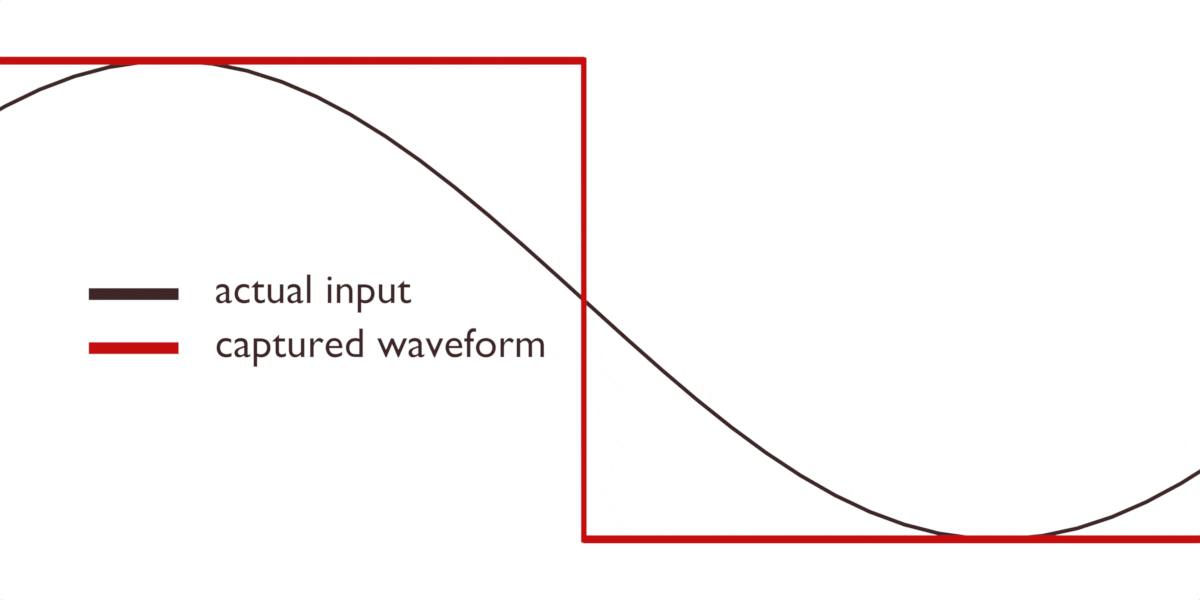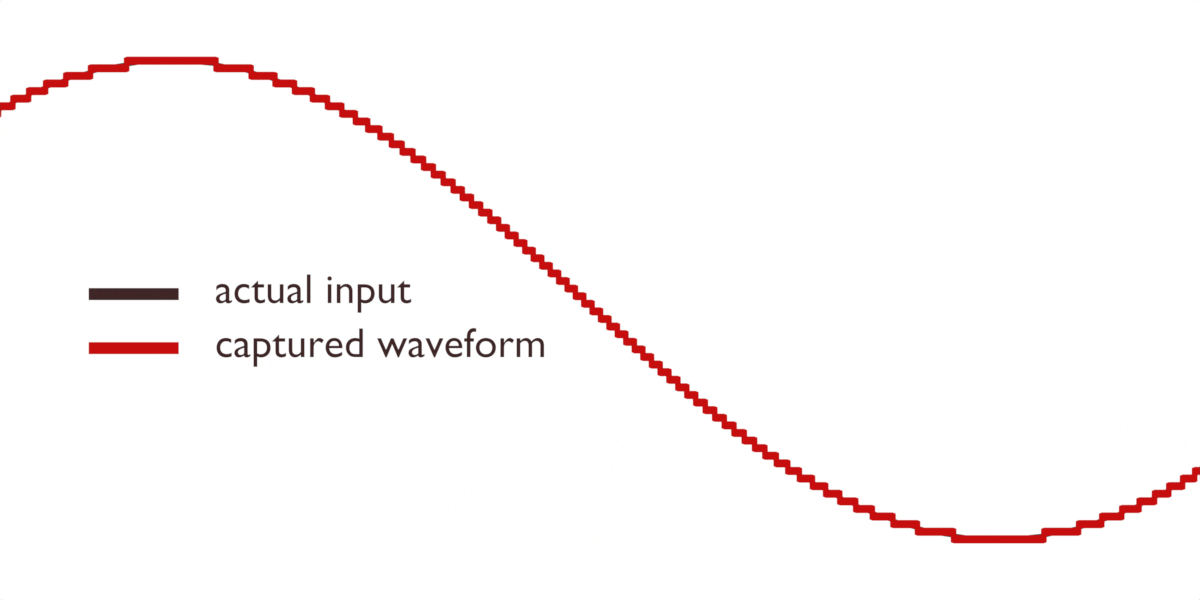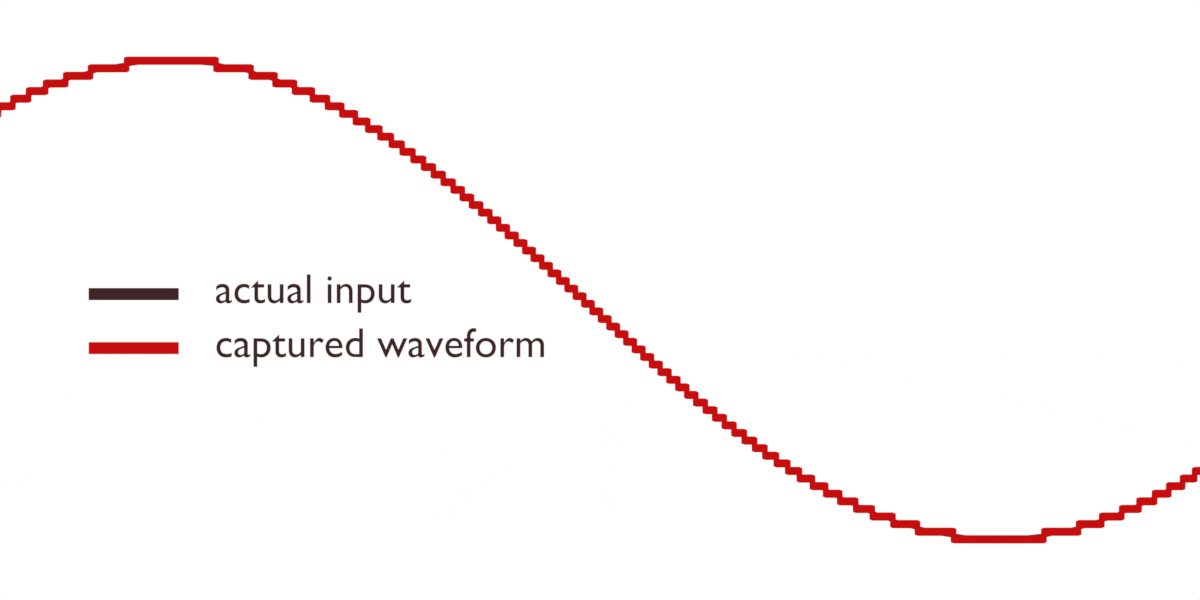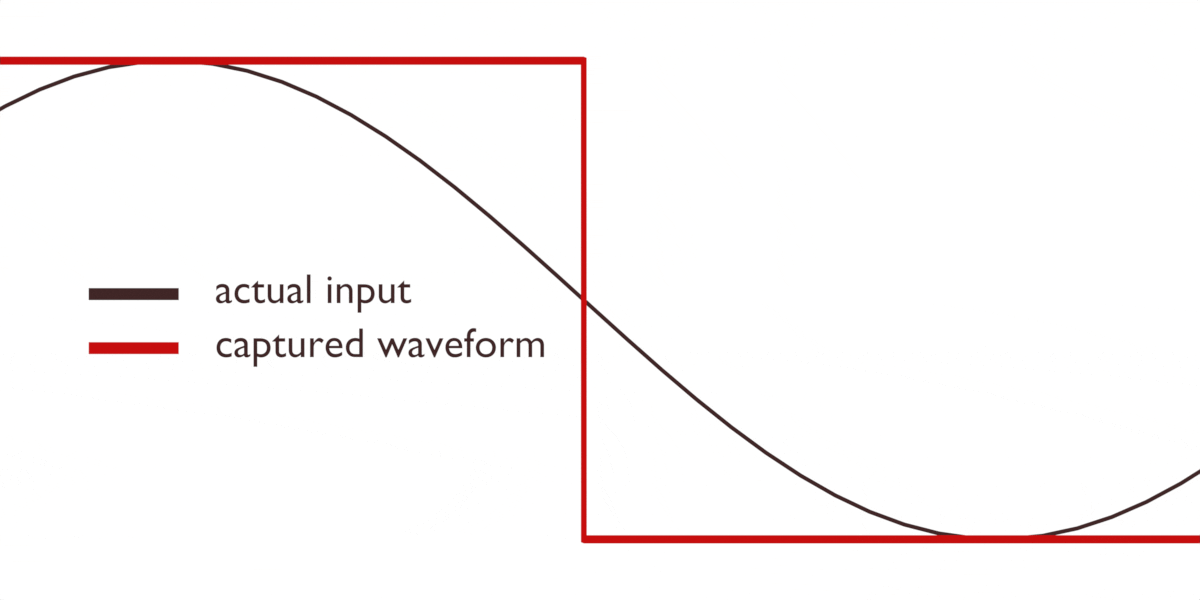
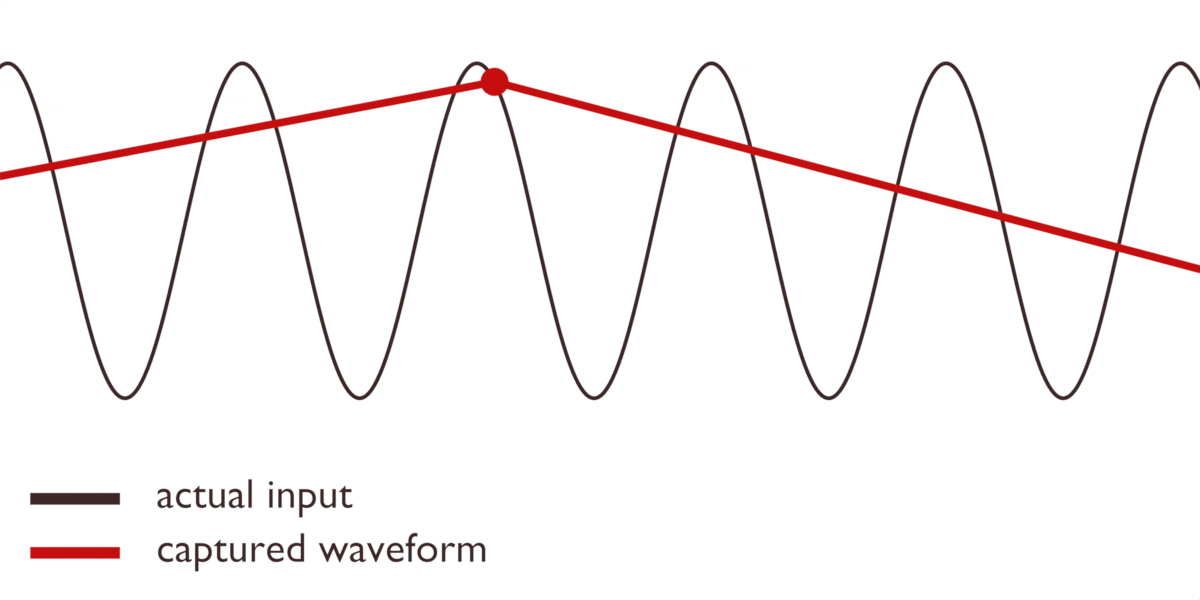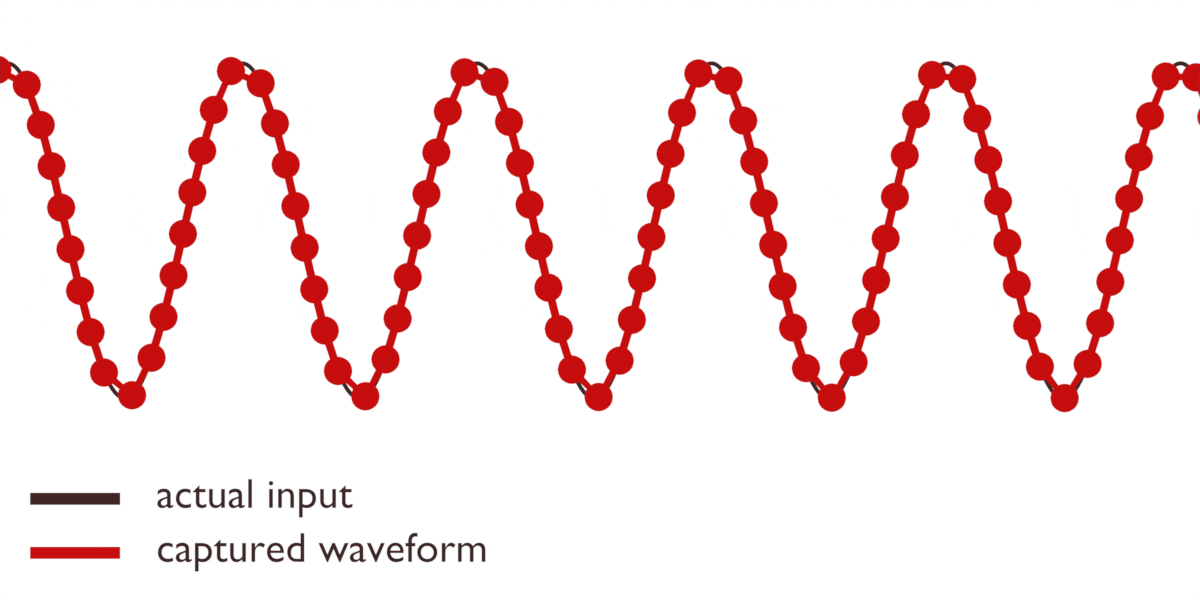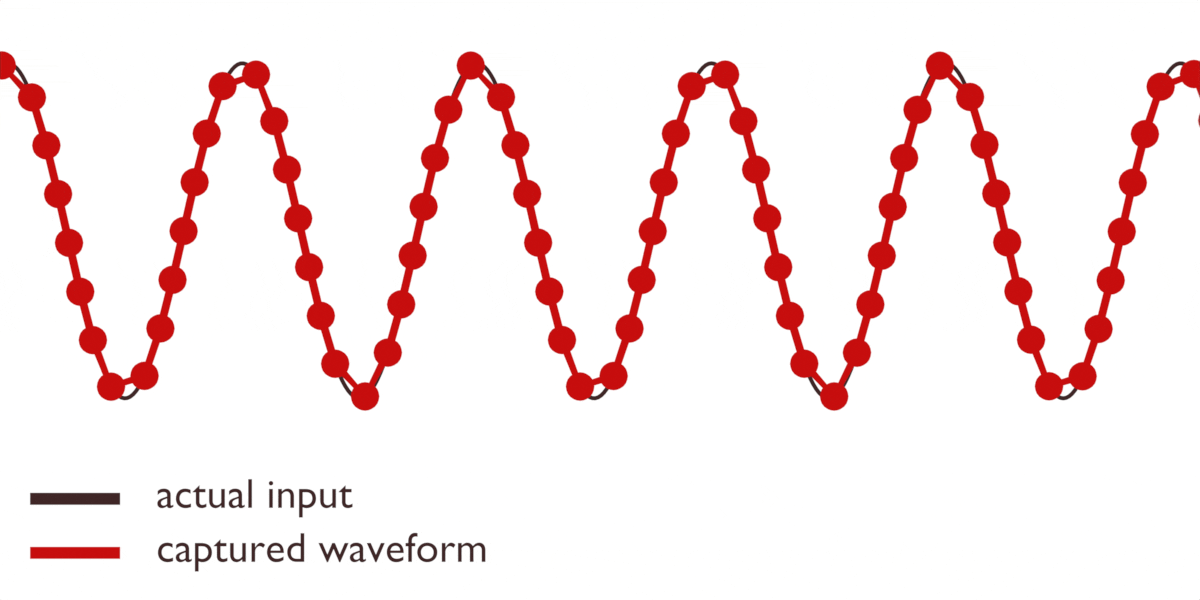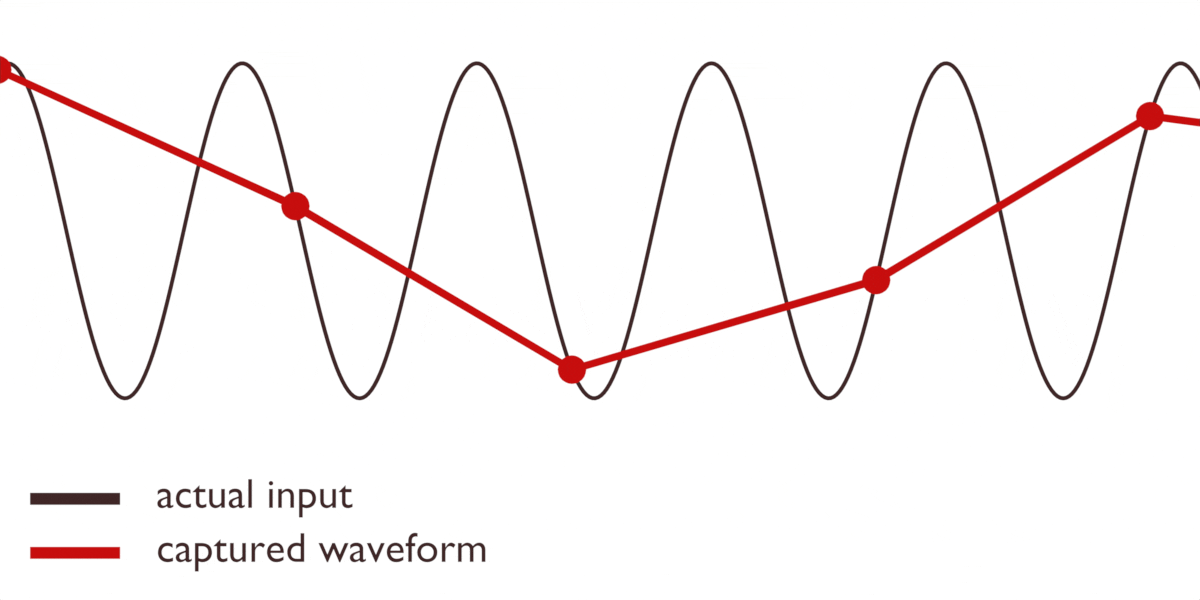
Oavsett vem vi ger äran till teorin, finns det ett problem. Det är omöjligt att i förväg veta exakt när en vågforms topp och botten kommer. Vad händer om vi tar våra avläsningar någonstans mitt i den inkommande vågformen? Lägg märke till hur en förändring i den inkommande signalen kan leda till att vårt fångade resultat blir helt platt:
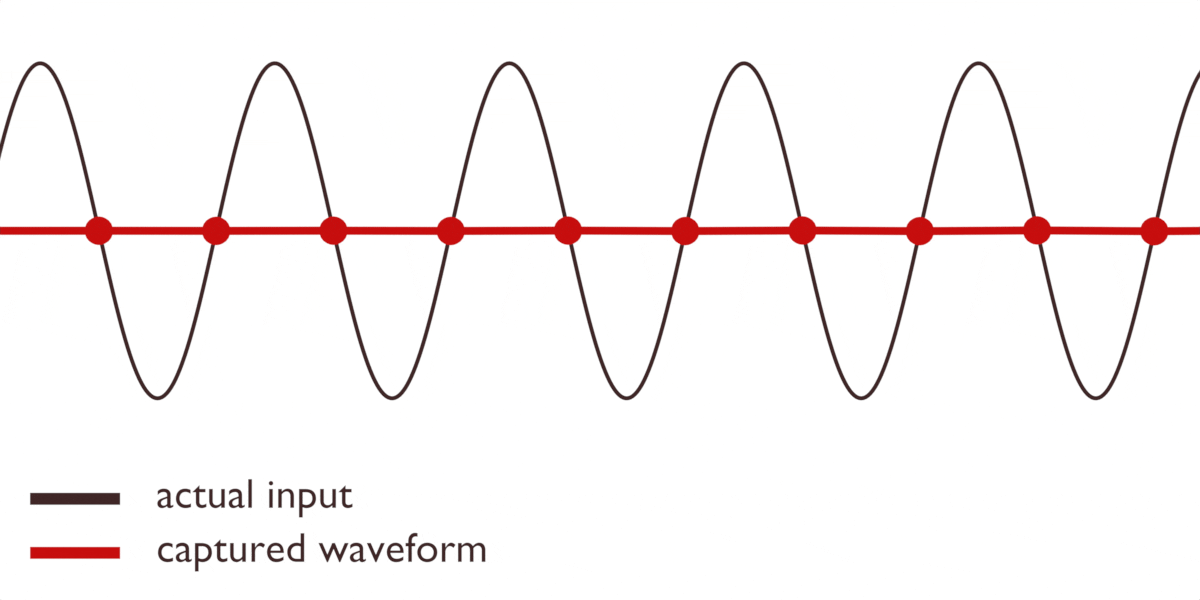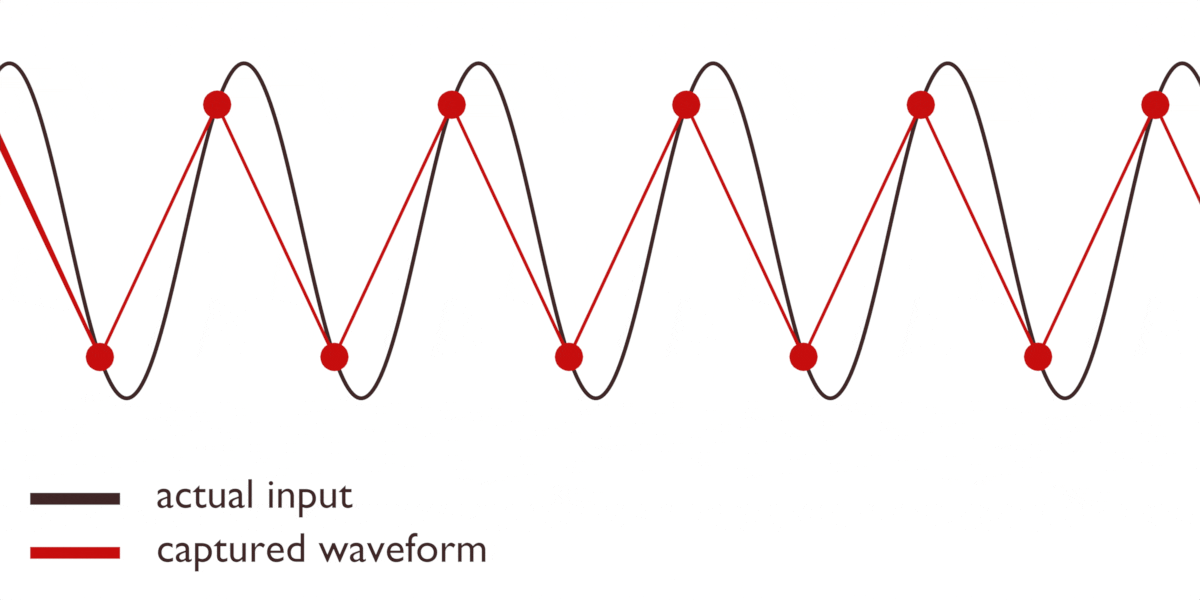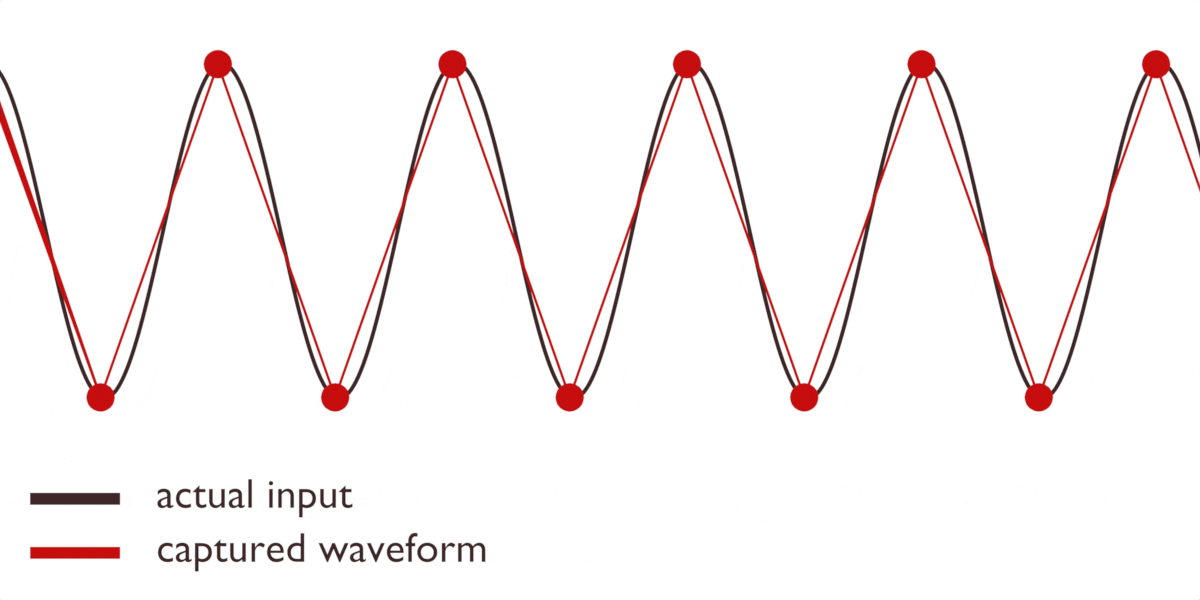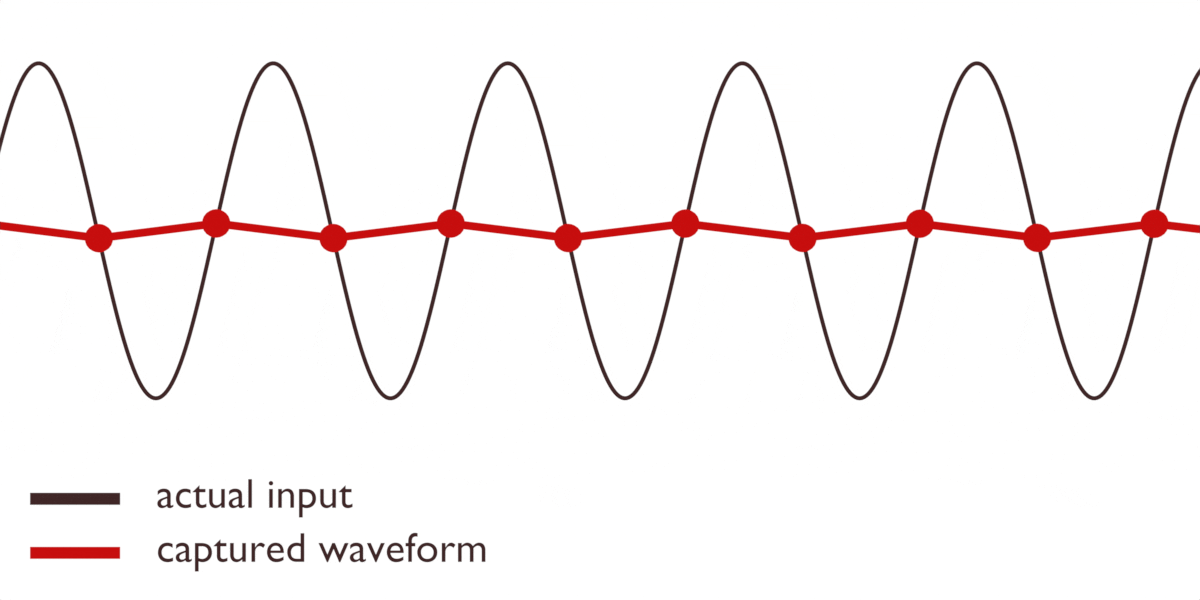
Eller att till och med skapa nya vågformer som inte existerade från början:
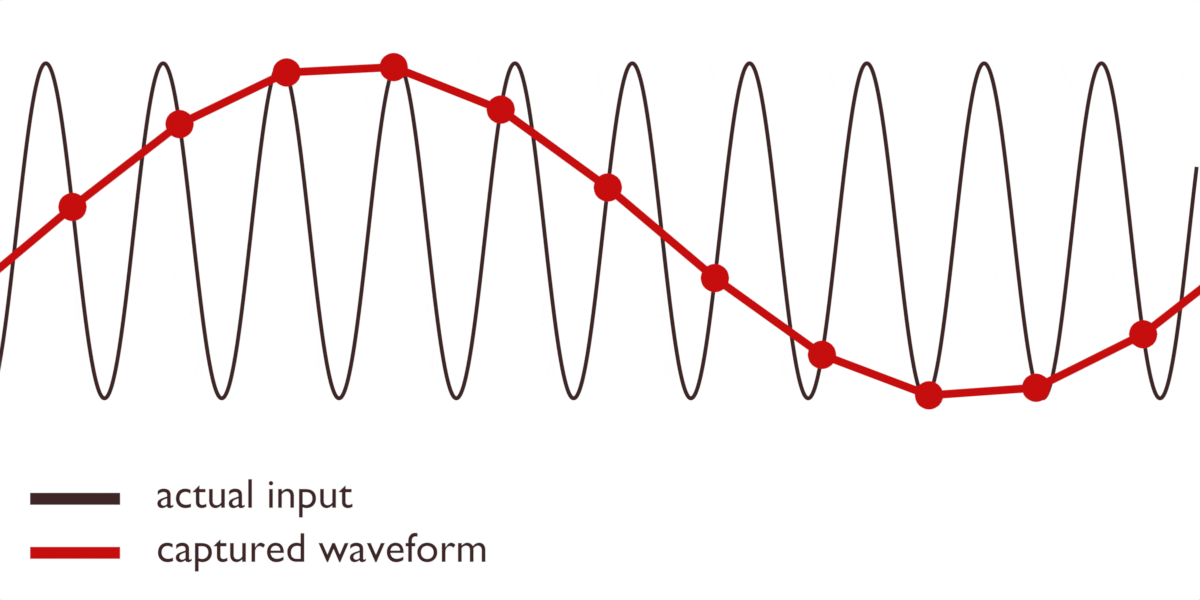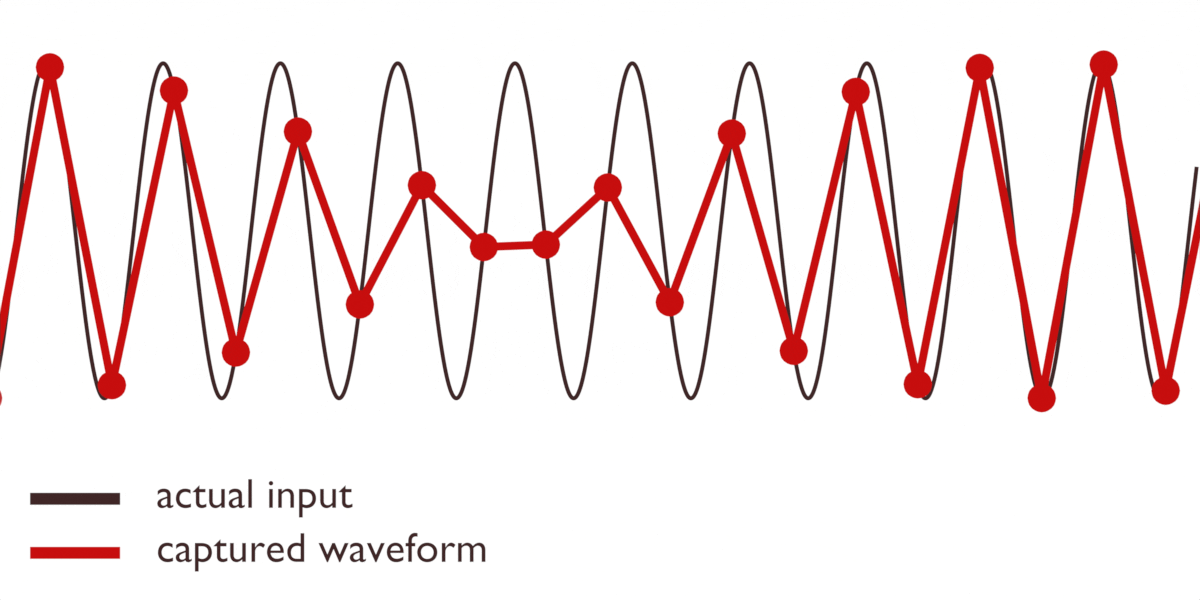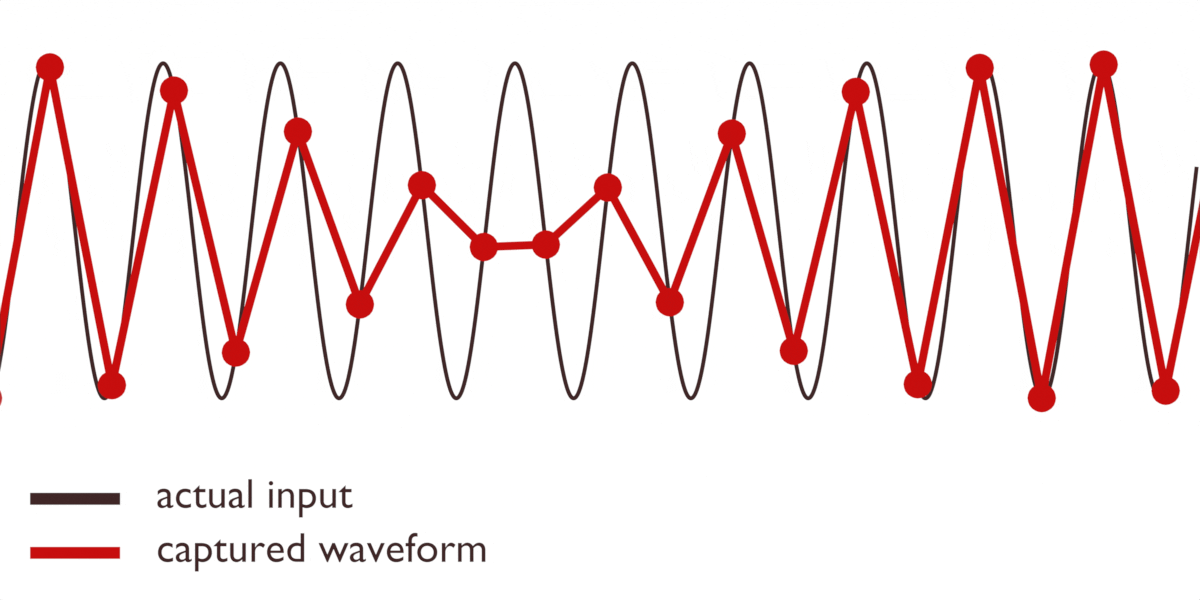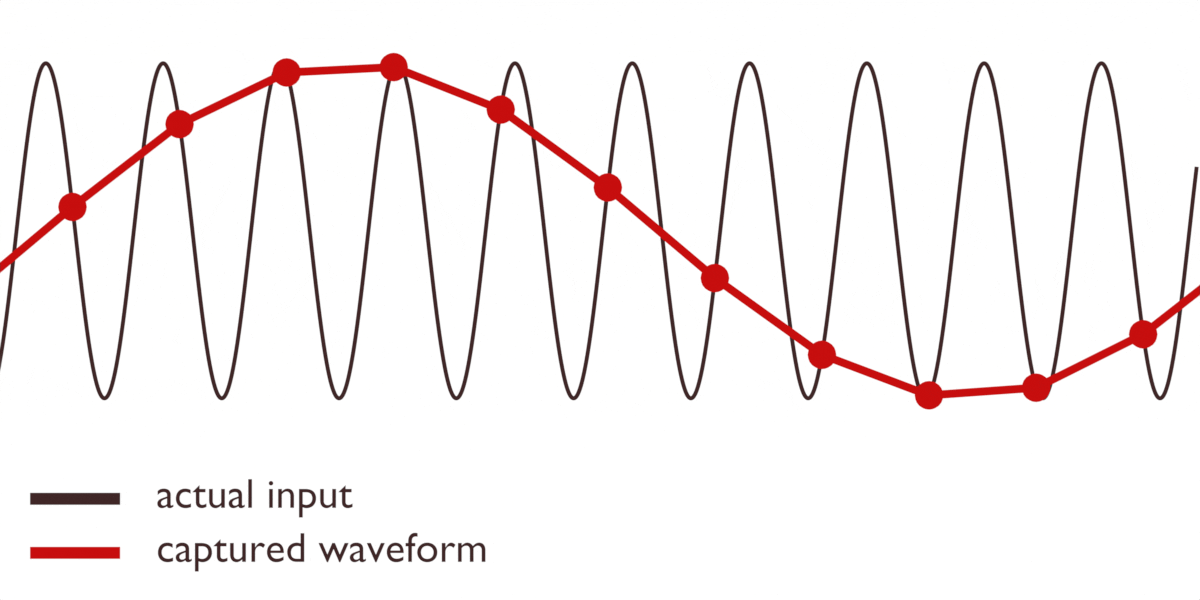
Dessa felaktiga representationer kallas för alias.
Problemet med alias
Du har säkert sett den så kallade ”vagn-hjul”-effekten som ibland uppstår när en roterande sak filmas. Bilhjul eller helikopterblad verkar rotera bakåt – om än mycket långsamt. I vissa fall kan bladen verka stå helt stilla (med märkliga resultat!).
När du spelar ett äldre videospel kanske du också har märkt att parallella linjer ibland skapar konstiga förvrängningar. Staket, trappor och randiga tröjor kan se konstiga ut. Eller de konstiga visslande ljud du ibland hör när du pratar med någon över en dålig digital förbindelse? Det är distorsion, men en speciell typ av distorsion. Vad händer med alla de fula frekvenserna som kommer från bruset? Om du lyssnar på komplext innehåll, som ett trumset, blir effekten ännu mer uppenbar – särskilt i de högre tonerna.
Om du förstår orsaken till en av dessa, är du på god väg att förstå dem alla. När det gäller vagnhjul innebär en fast bildhastighet att vi inte kan registrera rörelsen ordentligt. Om något roterar 350° per bildruta är det naturligt att uppfatta det som att det har flyttat sig 10° bakåt. Med andra ord, det finns inte tillräckligt med information för att korrekt återge vad som händer. Avläsningarna vi gör är inte synkroniserade med det vi försöker mäta.
Detta är inte ett problem som är unikt för analog-till-digital-omvandling. I många av dessa fall konverterar vi en typ av digital signal till en annan.
Så vad är lösningen? Det finns flera. Vi kan använda ett speciellt filter för att hantera dessa artefakter, vilket många ADC:er gör ”under huven”. Eller så kan vi ta många fler avläsningar än vad vi egentligen behöver. Ju fler avläsningar vi tar, desto mer exakt blir vår bild av vågen:
Bästa resultat med högre kvalitet på avläsningarna
Om du tycker att det här är intressant, finns det mycket att fördjupa sig i. ADC-enheter är mycket komplexa.
Men ur en vanlig användares, eller en genomsnittlig Arduino-entusiasts perspektiv är de också väldigt enkla. Spänningar matas in och siffror kommer ut. Så oavsett vad du försöker mäta – om det är fukthalten i jord, svängningarna i en röst eller en ström av ljus som bryts genom en lins – är chansen stor att det finns en ADC som passar jobbet.