Big O Cheat Sheet: Förklarat med Python-exempel

Innehållsförteckning

En Översikt av Big O-analys

Big O-analys är en metod för att utvärdera och jämföra effektiviteten hos olika algoritmer. Den hjälper oss att välja de algoritmer som är bäst lämpade för att hantera stora datamängder och som kan skala effektivt. Den här artikeln fungerar som en ”Big O Cheat Sheet”, där vi går igenom allt du behöver veta om Big O-notation.

Vad är Big O-analys?

Big O-analys fokuserar på att undersöka hur väl algoritmer presterar när datamängden ökar. Mer specifikt, vi vill veta hur algoritmens resursanvändning påverkas av en ökande datamängd.

Effektivitet handlar om hur väl systemresurserna används för att producera önskat resultat. De två viktigaste resurserna vi fokuserar på är tidsåtgång och minnesanvändning.

När vi utför Big O-analys, ställer vi oss följande frågor:

Hur påverkas en algoritms minnesanvändning när datamängden växer?
Hur påverkas den tid det tar för algoritmen att ge ett resultat när datamängden växer?

Svaret på den första frågan ger oss algoritmens rymdkomplexitet, och svaret på den andra frågan ger oss dess tidskomplexitet. Vi använder en speciell notation, Big O-notation, för att uttrycka dessa komplexiteter. Detta kommer att gås igenom mer detaljerat i detta ”Big O Cheat Sheet”.

Förutsättningar

För att fullt ut förstå och dra nytta av detta ”Big O Cheat Sheet”, är det bra att ha grundläggande kunskaper i algebra. Dessutom kommer vi att ge exempel i Python, så en viss förståelse för Python kan också vara till hjälp. Dock krävs ingen djupgående kunskap i programmering.

Hur man Utför Big O-analys

I det här avsnittet kommer vi att beskriva hur man genomför en Big O-analys.

Det är viktigt att notera att algoritmers prestanda kan variera beroende på hur indatan är strukturerad.

Till exempel är sorteringsalgoritmer som snabbast när listan redan är sorterad, vilket är det bästa scenariot. Om listan däremot är sorterad i omvänd ordning kommer samma sorteringsalgoritmer att vara som långsammast, vilket är det värsta scenariot.

När vi genomför Big O-analys, fokuserar vi enbart på det värsta scenariot.

Rymdkomplexitetsanalys

Låt oss börja med att titta på hur man analyserar rymdkomplexitet. Vi undersöker hur algoritmens extra minnesanvändning förändras när indatan växer.

Till exempel använder den rekursiva funktionen nedan en loop från n till noll. Dess rymdkomplexitet är direkt proportionell mot n. Detta beror på att antalet funktionsanrop på anropsstacken ökar i takt med att n växer. Därför har den en rymdkomplexitet av O(n).

def loop_recursively(n):
    if n == -1:
        return
    else:
        print(n)
        loop_recursively(n - 1)

En effektivare implementering kan se ut så här:

def loop_normally(n):
    count = n
    while count >= 0:
        print(count)
        count =- 1

I den här algoritmen använder vi endast en extra variabel för att loopa. Oavsett hur stort n blir, kommer vi fortfarande bara att använda en extra variabel. Därför har algoritmen konstant rymdkomplexitet, vilket betecknas med O(1).

Genom att jämföra rymdkomplexiteten hos de två algoritmerna, kan vi se att while-loopen är mer effektiv än rekursion. Detta är kärnan i Big O-analys: att undersöka hur algoritmers prestanda förändras med ökande indata.

Tidskomplexitetsanalys

När vi analyserar tidskomplexitet är vi intresserade av hur antalet beräkningssteg ökar, inte den totala tiden algoritmen tar. Detta beror på att den faktiska tiden påverkas av många systemrelaterade och slumpmässiga faktorer. Därför fokuserar vi på att spåra hur antalet beräkningssteg förändras, och antar att varje steg tar lika lång tid.

För att illustrera tidskomplexitetsanalys, betrakta följande exempel:

Antag att vi har en lista med användare, där varje användare har ett ID och ett namn. Vårt uppdrag är att skapa en funktion som returnerar användarens namn baserat på ett givet ID. Så här kan det se ut:

users = [
    {'id': 0, 'name': 'Alice'},
    {'id': 1, 'name': 'Bob'},
    {'id': 2, 'name': 'Charlie'},
]

def get_username(id, users):
    for user in users:
        if user['id'] == id:
            return user['name']
    return 'User not found'

get_username(1, users)

Med den här implementeringen går algoritmen igenom hela användarlistan för att hitta användaren med rätt ID. Om vi har 3 användare, utför algoritmen 3 iterationer. Om vi har 10 användare utförs 10 iterationer.

Därför ökar antalet steg linjärt med antalet användare. Den här algoritmen har linjär tidskomplexitet. Men vi kan göra det bättre.

Antag att vi istället för en lista, lagrade användarna i en ordlista. Då skulle algoritmen för att söka efter en användare se ut så här:

users = {
    '0': 'Alice',
    '1': 'Bob',
    '2': 'Charlie'
}

def get_username(id, users):
     if id in users:
         return users[id]
     else:
         return 'User not found'

get_username(1, users)

Med den här nya algoritmen, oavsett om vi har 3 eller 10 användare i ordlistan, skulle antalet steg som krävs för att hitta en användare vara ungefär detsamma. Antalet steg är konstant oavsett datamängdens storlek.

Därför har denna nya algoritm konstant tidskomplexitet. Antalet beräkningssteg förblir oförändrat oavsett antalet användare.

Vad är Big O-notation?

I det föregående avsnittet diskuterade vi hur man bedömer rymd- och tidskomplexiteten hos algoritmer och använde termer som ”linjär” och ”konstant”. Big O-notation är ett mer formellt sätt att beskriva komplexitet.

Big O-notation representerar en algoritms rymd- eller tidskomplexitet. Den består av ett O följt av parenteser, där vi inom parenteserna skriver en funktion av n som beskriver den specifika komplexiteten.

Linjär komplexitet representeras av n, så vi skriver det som O(n) (uttalas ”O av n”). Konstant komplexitet representeras av 1, så vi skriver det som O(1).

Det finns flera andra komplexiteter som vi kommer att gå igenom senare. Generellt sett, för att bestämma en algoritms komplexitet, följ dessa steg:

Försök att skapa en matematisk funktion av n, f(n), där f(n) representerar antalet beräkningssteg eller den mängd minne som används av algoritmen, och n är datamängdens storlek.
Välj den mest dominerande termen i funktionen. Domineringsordningen går från mest till minst dominant enligt följande: Faktoriell, Exponentiell, Polynom, Kvadratisk, Linjär-logaritmisk, Linjär, Logaritmisk och Konstant.
Ta bort eventuella koefficienter från termen.

Resultatet är den term som vi placerar inom parenteserna i Big O-notationen.

Exempel:

Betrakta följande Python-funktion:

users = [
    'Alice',
    'Bob',
    'Charlie'
]

def print_users(users):
    number_of_users = len(users)
    print("Total number of users:", number_of_users)

    for i in range(number_of_users):
        print(i, end=': ')
        print(users[i])

Låt oss beräkna algoritmens Big O-tidskomplexitet.

Först skapar vi en matematisk funktion av n, f(n), för att representera antalet beräkningssteg. Kom ihåg att n representerar datamängdens storlek.

Funktionen utför två initiala steg: ett för att hämta antalet användare och ett för att skriva ut antalet användare. Sedan, för varje användare, utför den två steg: ett för att skriva ut indexet och ett för att skriva ut användaren.

Därför kan funktionen för att representera antalet beräkningssteg skrivas som f(n) = 2 + 2n, där n är antalet användare.

I steg två väljer vi den mest dominerande termen. 2n är en linjär term och 2 är en konstant term. Linjär dominerar över konstant, så vi väljer 2n.

Vår funktion är nu f(n) = 2n.

Det sista steget är att eliminera koefficienter. I vår funktion har vi 2 som koefficient. Vi tar bort den, och funktionen blir f(n) = n. Detta är termen vi använder inom parenteserna.

Därför är tidskomplexiteten för algoritmen O(n), eller linjär komplexitet.

Olika Big O-komplexiteter

I det här avsnittet ska vi gå igenom olika typer av komplexitet och deras motsvarande grafer.

#1. Konstant

Konstant komplexitet innebär att algoritmen använder en konstant mängd minne (vid analys av rymdkomplexitet) eller utför ett konstant antal steg (vid analys av tidskomplexitet). Detta är den mest optimala komplexiteten, eftersom algoritmen inte kräver mer minne eller tid när indatan växer. Den är därför mycket skalbar.

Konstant komplexitet representeras som O(1). Det är dock inte alltid möjligt att skapa algoritmer som har konstant komplexitet.

#2. Logaritmisk

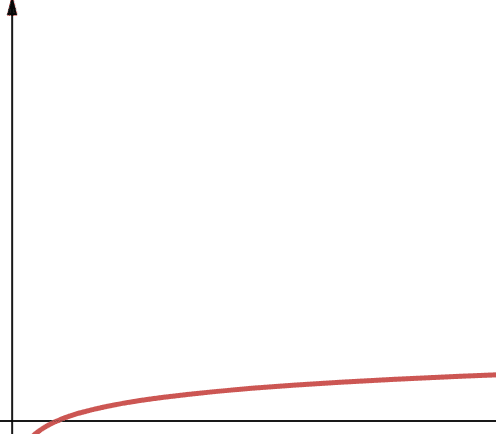
Logaritmisk komplexitet representeras med O(log n). Om basen för logaritmen inte anges inom datavetenskap, antas den vara 2.

Därför är log n detsamma som log₂n. Logaritmiska funktioner ökar snabbt i början men saktar sedan ner. Det innebär att de skalar effektivt med ökande n.

#3. Linjär

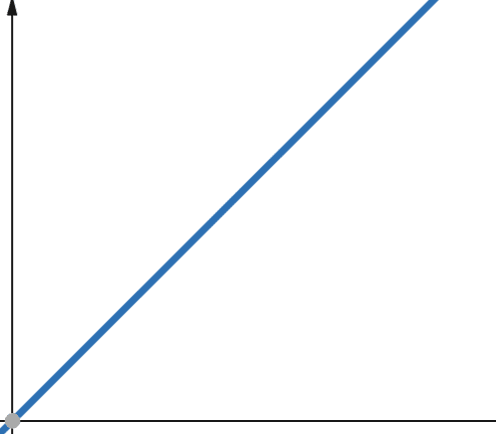
Med linjära funktioner, om den oberoende variabeln ökar med en faktor p, så ökar även den beroende variabeln med samma faktor p.

En funktion med linjär komplexitet växer alltså i samma takt som datamängden. Om indatastorleken fördubblas, kommer antalet beräkningssteg eller minnesanvändningen också att fördubblas. Linjär komplexitet betecknas med O(n).

#4. Linjär-logaritmisk

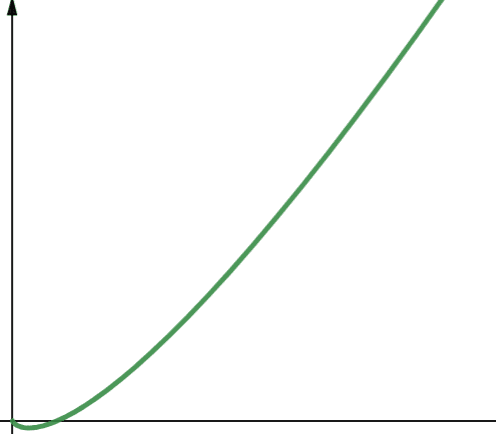
O(n * log n) representerar linjär-logaritmiska funktioner. En linjär-logaritmisk funktion är en linjär funktion multiplicerad med en logaritmisk funktion. Detta ger resultat som är något högre än linjära funktioner när log n är större än 1. Detta beror på att n multipliceras med ett tal större än 1.

Log n är större än 1 för alla värden på n som är större än 2 (kom ihåg att log n = log₂n). Därför är linjär-logaritmiska funktioner i allmänhet mindre skalbara än logaritmiska funktioner.

#5. Kvadratisk

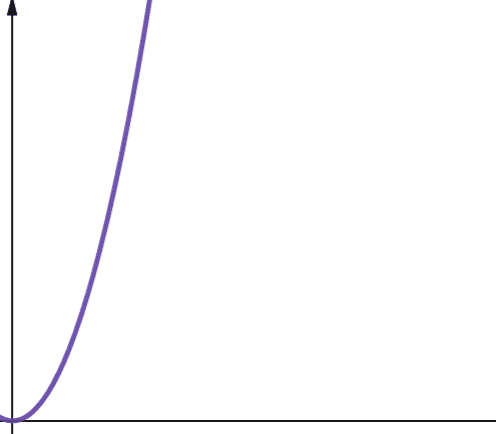
Kvadratisk komplexitet representeras av O(n²). Om din datamängd ökar med en faktor 10, ökar antalet steg eller minnesanvändningen med 10², vilket är 100! Den här typen av komplexitet är inte särskilt skalbar och ökar mycket snabbt.

Kvadratisk komplexitet uppstår i algoritmer där du loopar n gånger, och för varje iteration loopar du n gånger till, som till exempel i Bubble Sort. Även om det i allmänhet inte är idealiskt, kan det ibland vara nödvändigt att använda algoritmer med kvadratisk komplexitet.

#6. Polynom

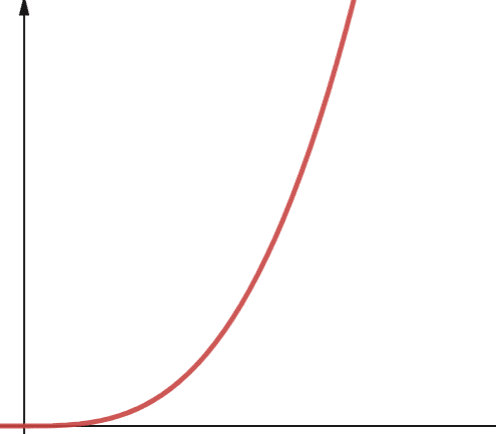
En algoritm med polynomkomplexitet representeras av O(n^p), där p är ett konstant heltal. P representerar ordningen i vilken n är upphöjd.

Denna komplexitet uppstår när du har flera kapslade loopar. Skillnaden mellan polynomkomplexitet och kvadratisk komplexitet är att kvadratisk komplexitet är av ordningen 2, medan polynomkomplexitet kan ha ett valfritt tal större än 2.

#7. Exponentiell

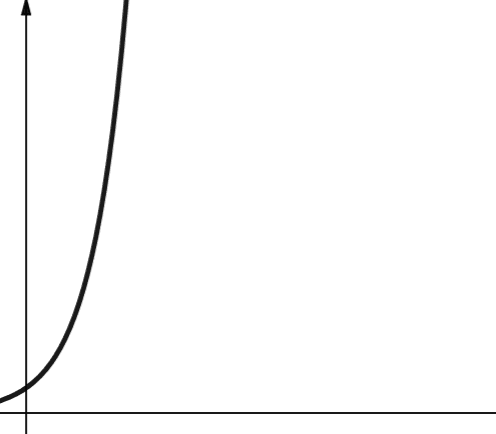
Exponentiell komplexitet växer ännu snabbare än polynomkomplexitet. I matematik är standardvärdet för exponentialfunktionen konstanten e (Eulers tal). Men inom datavetenskap är standardvärdet för exponentialfunktionen 2.

Exponentiell komplexitet representeras med O(2ⁿ). När n är 0, är 2ⁿ 1. Men när n ökar till 5, ökar 2ⁿ till 32. En ökning av n med ett dubblar det föregående värdet. Exponentiella funktioner är därför inte särskilt skalbara.

#8. Faktoriell

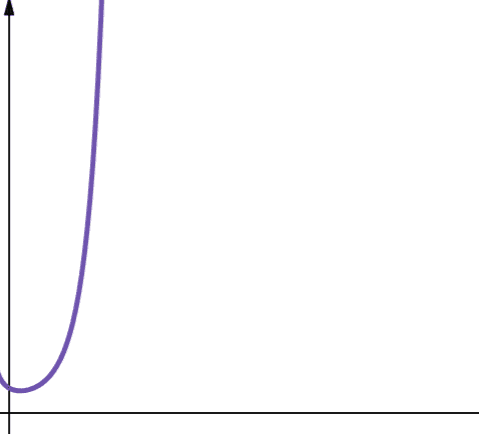
Faktoriell komplexitet representeras av O(n!). Denna funktion ökar mycket snabbt och är därför inte skalbar.

Slutsats

Den här artikeln har gett en översikt över Big O-analys och hur man beräknar den. Vi har diskuterat olika komplexiteter och deras skalbarhet.

För att vidareutveckla dina kunskaper kan du öva på Big O-analys med olika sorteringsalgoritmer i Python.