Sedan den initiala tanken om en kvantdator presenterades 1980, har kvantdatorindustrin genomgått en kraftig tillväxt, särskilt under det senaste decenniet. Idag engagerar sig en rad företag i utvecklingen av kvantdatorer.
Kvantberäkning kan vara svår att greppa för många, och mycket information på området lyckas inte förmedla de väsentliga detaljerna på ett tydligt sätt.
Den här texten strävar efter att reda ut begreppen. Genom att läsa hela artikeln kommer du att erhålla en djupgående förståelse för vad kvantberäkning innebär, olika varianter av kvantberäkningar, deras funktion, algoritmer, modeller, strategier, utmaningar och användningsområden.
Vad är kvantdatorer?
Kvantdatorer angriper problem på ett sätt som skiljer sig från de datorer vi är vana vid, vilka jag hädanefter kommer att kalla klassiska datorer.
Kvantdatorer besitter vissa fördelar jämfört med konventionella datorer när det gäller att hantera vissa typer av problem. Detta härrör från deras kapacitet att existera i ett stort antal tillstånd samtidigt, medan klassiska datorer endast kan befinna sig i ett enskilt tillstånd åt gången.
Bildkälla: IBM
För att förstå detta, samt hur kvantdatorer fungerar, behöver man bekanta sig med tre grundläggande koncept: superposition, sammanflätning och interferens.
Klassiska datorers grundenhet är bitar, medan kvantdatorer använder kvantbitar, eller qubits. Dessa enheter fungerar enligt fundamentalt olika principer.
En klassisk bit kan liknas vid en strömbrytare som antingen kan inta tillståndet 0 eller 1, vilket troligen är bekant som binär information. Vid mätning av en bit erhålls alltid det tillstånd som den befinner sig i. För qubits är situationen annorlunda. En qubit är mer komplex.
Superposition
För en åskådlig visualisering kan man tänka sig en pil som pekar i tre dimensioner. Om pilen pekar rakt upp representerar det tillståndet 1, och rakt ner representerar 0, likt en klassisk bit. Men de har också förmågan att befinna sig i ett så kallat superpositionstillstånd, vilket inträffar när pilen pekar i någon annan riktning.
Detta superpositionstillstånd är en kombination av tillstånden 0 och 1.
Superposition tillstånd
När en qubit mäts kommer resultatet fortfarande vara antingen 1 eller 0, men utfallet bestäms av en sannolikhet som styrs av pilens riktning.
Om pilen lutar mer uppåt är det mer sannolikt att 1 mäts, jämfört med 0. Om pilen pekar mer neråt är det tvärtom. Om pilen befinner sig precis på ekvatorn är det lika sannolikt att antingen 0 eller 1 mäts (50% sannolikhet).
Detta är effekten av superposition. Låt oss nu övergå till sammanflätning.
Sammanflätning
I klassiska datorer är bitarna fullständigt oberoende av varandra. En bits tillstånd påverkas inte av tillståndet hos andra bitar. I kvantdatorer kan qubits däremot vara sammanflätade, vilket innebär att de blir en del av ett gemensamt kvanttillstånd.
Betrakta till exempel två qubits som båda befinner sig i olika superpositionstillstånd, men som ännu inte är sammanflätade. Sannolikheterna för varje qubit är i nuläget oberoende av varandra.
Men när vi sammanflätar dem, upphör de individuella sannolikheterna att gälla. Istället måste vi beräkna en sannolikhetsfördelning av alla möjliga tillstånd: 00, 01, 10 eller 11.
Det centrala är att när qubits är sammanflätade, så påverkar ändringen av pilens riktning på en qubit sannolikhetsfördelningen för hela systemet. Qubits är inte längre oberoende av varandra, utan del av ett gemensamt tillstånd.
Detta gäller oavsett antalet qubits. För en qubit har vi en sannolikhetsfördelning över två tillstånd.
För två qubits finns sannolikhetsfördelningen över fyra tillstånd. För tre qubits är det åtta tillstånd, och antalet fördubblas för varje ytterligare qubit.
Generellt kan en kvantdator med n qubits befinna sig i en kombination av 2^n tillstånd. Det är denna skillnad som utgör kärnan i skillnaden mellan klassiska datorer och kvantdatorer.
Klassiska datorer kan befinna sig i vilket tillstånd som helst, men endast ett i taget. Kvantdatorer kan befinna sig i en superposition av alla dessa tillstånd samtidigt.
Frågan är hur ett superpositionstillstånd kan vara användbart i en dator. Svaret finns i den sista komponenten: Interferens.
Interferens
För att illustrera effekten av interferens, måste vi återgå till bilden av en qubit, som tekniskt kallas en Bloch-sfär. En qubit ser inte fysiskt ut som en sådan, utan detta är ett sätt att visualisera tillståndet hos en qubit.
I realiteten beskrivs en qubits tillstånd av en mer abstrakt enhet kallad kvantvågfunktion. Vågfunktioner är den fundamentala matematiska beskrivningen inom kvantmekaniken.
När många qubits är sammanflätade, adderas samtliga vågfunktioner för att bilda en övergripande vågfunktion som beskriver kvantdatorns tillstånd.
Denna addition av vågfunktioner är interferens. Likt vågor på vattenytan kan vågor konstruktivt interferera och förstärka varandra. De kan även destruktivt interferera och utsläcka varandra.
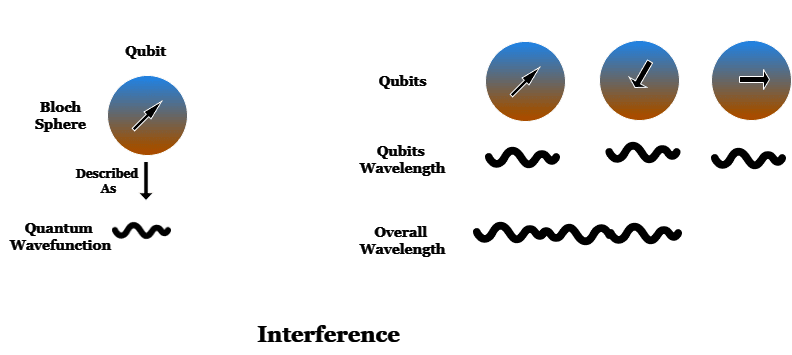
Kvantdatorns övergripande vågfunktion bestämmer sannolikheterna för de olika tillstånden. Genom att ändra tillstånden för olika qubits kan man anpassa sannolikheterna för att olika tillstånd ska manifesteras vid mätning av kvantdatorn.
Kom ihåg att trots att kvantdatorn kan befinna sig i en superposition av miljontals tillstånd samtidigt, så erhålls endast ett enskilt tillstånd vid mätning.
Vid användning av en kvantdator för att lösa ett beräkningsproblem, ska konstruktiv interferens användas för att öka sannolikheten för det rätta svaret. Destruktiv interferens används för att minska sannolikheten för felaktiga svar, så att det korrekta svaret kommer fram vid mätning.
Kvantalgoritmer
Sättet detta åstadkoms ligger inom kvantalgoritmernas område. Hela motivationen bakom kvantberäkning är att det teoretiskt finns en mängd problem som kan lösas på en kvantdator, men anses vara extremt svåra att hantera på klassiska datorer.
Låt oss granska några av dem. Det finns många kvantalgoritmer, för många för att gå igenom i den här texten. Vi kommer att fokusera på den mest kända och historiskt betydelsefulla: Shors algoritm.
#1. Shors algoritm
Om två stora tal multipliceras, finns en snabb och effektiv klassisk algoritm för att hitta produkten. Men om man utgår från produkten och söker efter de ursprungliga talen, så blir problemet mycket svårare.
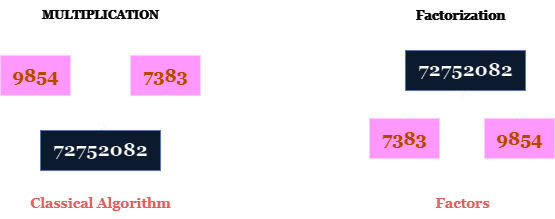
Denna operation kallas faktorisering. Siffrorna i produkten kallas faktorer. Anledningen till att de är så svåra att hitta är att sökutrymmet för möjliga faktorer är så enormt. Det finns ingen effektiv klassisk algoritm för att hitta faktorer för stora tal.
Av den anledningen används den matematiska egenskapen för internetkryptering: säkra hemsidor, e-post och bankkonton. Om faktorerna är kända, är informationen enkel att dekryptera. Om de är okända, måste de beräknas först, vilket är extremt svårt även för världens mest kraftfulla datorer.
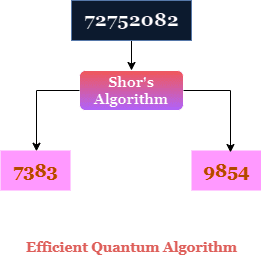Shors algoritm
År 1994 publicerade Peter Shor en snabb kvantalgoritm som effektivt kunde hitta faktorer för stora heltal. Det orsakade stor uppmärksamhet.
Detta var ögonblicket när många började ta kvantberäkning på allvar. Det var det första verkliga problemet med potentiella enorma säkerhetskonsekvenser som en kvantalgoritm kunde lösa.
När det talas om en ”snabb” kvantalgoritm, hur mycket snabbare är den jämfört med en klassisk dator? För att besvara det, behöver vi ta en liten avstickare till kvantkomplexitetsteorins värld.
Kvantkomplexitetsteori
Kvantkomplexitetsteori är en gren av beräkningskomplexitetsteorin. Den handlar om att kategorisera algoritmer. Algoritmer sorteras efter hur väl de fungerar på datorer.
Klassificeringen bestäms av den ökande svårighetsgraden att lösa ett problem när det blir större. Alla problem inom P-rutan är enkla för klassiska datorer att lösa. Utanför rutan finns de problem där vi inte har effektiva klassiska algoritmer. Faktorisering av stora tal hör till den senare kategorin.
Men det finns även en cirkel, BQP, som representerar problem som är effektiva för kvantdatorer men inte för klassiska datorer. Det är dessa problem som kvantdatorer förväntas vara överlägsna klassiska datorer att lösa.
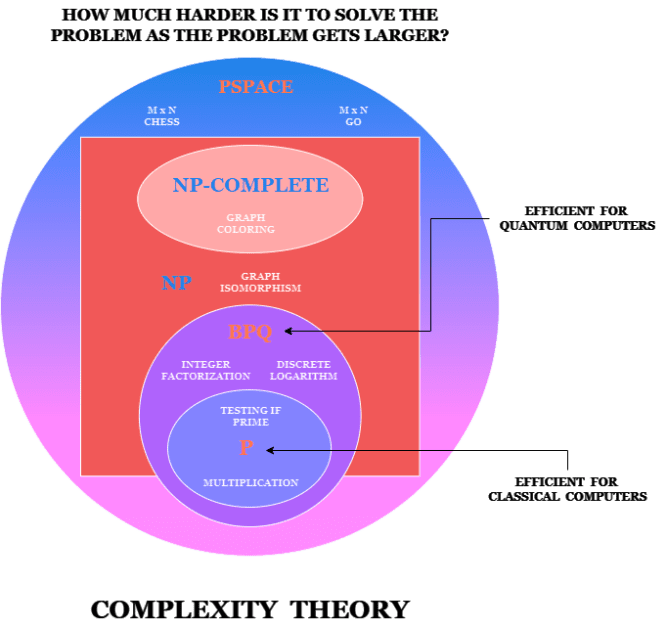
Komplexitetsteorin undersöker hur svårt det är att lösa ett problem när problemet blir större. Om vi faktoriserar ett tal med åtta siffror, hur mycket svårare är det att faktorisera ett tal med nio siffror? Är det dubbelt så svårt?
Eller exponentiellt svårare? Och hur ser trenden ut med allt fler siffror? Detta är vad som kallas komplexitet eller skalning, och för faktorisering är den exponentiell.
Allt med N i exponenten är exponentiellt svårt. Exponentiella problem blir snabbt mycket svåra att lösa när problemen växer i storlek. Inom datavetenskap vinner man respekt och rykte om man kan hitta en bättre algoritm för att lösa dessa svåraste problem.
Ett exempel på det var Shors algoritm. Algoritmen utnyttjar kvantdatorers speciella egenskaper för att skapa en algoritm med mycket bättre skalning än den bästa klassiska algoritmen.
Den bästa klassiska algoritmen är exponentiell, medan Shors algoritm är polynomisk, vilket är ett viktigt steg i komplexitetsteori och datavetenskap generellt, eftersom det omvandlar ett olösbart problem till ett lösbart.
Lösbart, det vill säga om en fungerande kvantdator finns tillgänglig. Det är vad många arbetar på att utveckla. Det finns ännu ingen anledning att oroa sig för säkerheten för bankkonton, eftersom dagens kvantdatorer inte kan köra Shors algoritm på stora tal.
IBM Quantum
Det skulle krävas många qubits för att göra det. De mest avancerade universella kvantdatorerna har idag cirka 433.
Dessutom arbetar man på så kallade post-kvantkrypteringsscheman som inte använder heltalssaktorisering. Teknik från kvantfysikens värld kan också hjälpa till, genom ett kryptografiskt system kallat kvantkryptografi.
Detta var en överblick av en kvantalgoritm. Det finns många fler, alla med sina egna egenskaper.
#2. Grovers algoritm
Ett annat anmärkningsvärt exempel är Grovers algoritm, som kan söka i ostrukturerade datalistor snabbare än den bästa klassiska algoritmen.
Det är viktigt att inte felaktigt karaktärisera klassiska datorer. De är mångsidiga enheter och det finns inget som hindrar någon från att hitta en smart klassisk algoritm som kan lösa de svåraste problemen som heltalssaktorisering mer effektivt.
Många tror att det är osannolikt, men inte omöjligt. Det finns också problem som bevisligen inte går att lösa med klassiska datorer. Dessa så kallade icke-beräkningsbara problem, som stoppproblemet, går inte heller att lösa med kvantdatorer.
Beräkningsmässigt är klassiska datorer och kvantdatorer likvärdiga. Skillnaderna uppstår i algoritmerna de kan köra. Det är till och med möjligt att simulera en kvantdator på en klassisk dator och vice versa.
Att simulera en kvantdator på en klassisk dator blir exponentiellt mer utmanande när antalet simulerade qubits ökar.
Detta beror på att klassiska datorer kämpar med att simulera kvantsystem. Kvantdatorer däremot, som är kvantsystem, har inte det problemet. Det leder mig till min favoritapplikation för kvantdatorer: kvantsimulering.
#3. Kvantsimulering
Kvantsimulering innebär att man simulerar saker som kemiska reaktioner eller elektroners beteende i olika material. Inom detta område har kvantdatorer en exponentiell fördel jämfört med klassiska datorer, eftersom dessa kämpar för att simulera kvantsystem.
Att simulera kvantsystem, även med få partiklar, är svårt även med världens mest kraftfulla superdatorer. Vi kan ännu inte göra det på kvantdatorer, men när de blir mer mogna är ett huvudmål att simulera allt större kvantsystem.
Detta inkluderar områden som beteendet hos exotiska material vid låga temperaturer, förståelsen av varför vissa material blir supraledande, samt att studera viktiga kemiska reaktioner för att förbättra deras effektivitet. Ett exempel är att producera gödsel med mycket mindre koldioxidutsläpp, eftersom gödselproduktion står för cirka 2% av de globala koldioxidutsläppen.
Du kan lära dig mer om kvantkemisk simulering på djupet.
Kvantsimulering
Andra potentiella användningsområden för kvantsimulering inkluderar att förbättra solpaneler, batterier och utveckla nya läkemedel, kemikalier eller material för flyg.
Generellt skulle kvantsimulering möjliggöra snabb prototypframställning av många olika material i en kvantdator. Deras fysiska parametrar kan testas, istället för att fysiskt tillverka och testa dem i ett labb. Den processen är mycket mer kostsam och tidskrävande.
Detta har potential att avsevärt påskynda processer och generera betydande tids- och kostnadsbesparingar. Det är viktigt att betona att dessa är potentiella användningsområden. Det finns ännu inga kvantdatorer som kan lösa verkliga problem bättre än våra vanliga datorer. Men det är just den här typen av problem som kvantdatorer skulle vara väl lämpade för.
Modeller av kvantdatorer
Inom kvantdatorernas värld finns det en stor variation av strategier för att omvandla olika kvantsystem till kvantdatorer. Det finns två nivåer av nyanser som behöver diskuteras.
Kretsmodellen
I kretsmodellen samverkar qubits med speciella grindar som påverkar några qubits åt gången och ändrar deras tillstånd utan att de observeras. Grindarna placeras i en specifik ordning för att skapa en kvantalgoritm. Slutligen mäts qubits för att erhålla det önskade svaret.
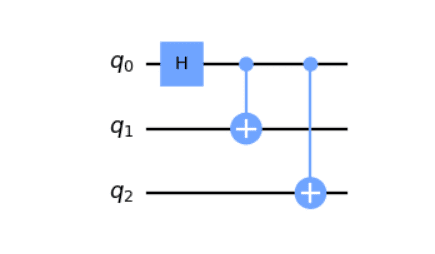Bildkredit: qiskit
Adiabatisk kvantberäkning
Inom adiabatisk kvantberäkning utnyttjar man en grundläggande fysikalisk princip. Alla system strävar mot det minimala energitillståndet. Adiabatisk kvantberäkning fungerar genom att rama in problem så att kvantsystemets lägsta energitillstånd representerar lösningen.
Kvantglödgning
Kvantglödgning är inte ett universellt kvantberäkningsschema. Det bygger på samma princip som adiabatisk kvantberäkning, där systemet hittar det lägsta energitillståndet för en energilandskap som presenteras för systemet.
Topologisk kvantberäkning
I det topologiska tillvägagångssättet byggs qubits från en entitet inom fysiken kallad Majorana-nollmods-kvasipartikel. Den är en typ av icke-abelisk anyon. Kvasipartiklarna förväntas vara stabilare på grund av deras fysiska åtskillnad.
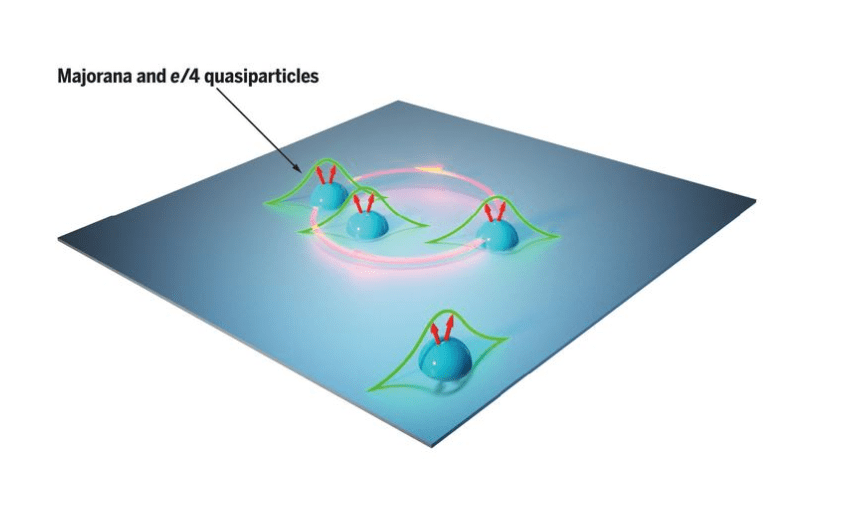Bildkredit Civilsday
Utmaningar inom konstruktionen
Oavsett metod, finns det liknande utmaningar.
- Dekoherens: Det är svårt att kontrollera kvantsystem. Vid minsta interaktion med omvärlden börjar information läcka bort. Det kallas dekoherens. Qubits är gjorda av fysiska ting och kräver fysiska ting för att kontrollera och mäta dem. Qubits är ”dumma” och kan bli sammanflätade med allt i deras omgivning. Qubits måste konstrueras noggrant för att skydda dem från att bli sammanflätade med sin omgivning.
- Brus: Qubits måste skyddas från alla typer av brus. Det kan vara kosmisk strålning, värmeenergi eller vilsepartiklar. En viss mängd dekoherens och brus är oundvikligt i alla fysiska system och omöjliga att helt eliminera.
- Skalbarhet: För varje qubit krävs en uppsättning kablar för att manipulera och mäta den. När fler qubits läggs till ökar den nödvändiga infrastrukturen linjärt. Varje kvantdator behöver hitta ett sätt att effektivt sammanfläta, kontrollera och mäta alla qubits när den skalas upp.
- Kvantfelkorrigering: Kvantfelkorrigering är ett system som gör kvantdatorer feltoleranta. Ett stort antal sammanflätade qubits används för att representera en brusfri qubit. Det krävs alltså ett stort antal fysiska qubits för att göra en enda feltolerant qubit.
Fysiska implementeringar
Det finns en stor variation av fysiska implementeringar för kvantdatorer, eftersom det finns många olika kvantsystem som kan användas. Här är några av de vanligaste och mest framgångsrika metoderna:
- Supraledande kvantdatorer: Supraledande qubits är i nuläget det vanligaste tillvägagångssättet. Qubits är gjorda av supraledande ledningar med en avbrott i ledaren som kallas Josephson-övergång. Den mest populära typen av supraledande qubit kallas transmon.
- Quantum Dot-kvantdatorer: Qubits är gjorda av elektroner eller grupper av elektroner. Tvånivåsystemet är kodat i elektronernas spinn eller laddning. Dessa qubits är konstruerade av halvledare, som kisel.
- Linjär optisk kvantberäkning: Optiska kvantdatorer använder fotoner av ljus som qubits. Dessa qubits påverkas genom optiska element som speglar, vågplattor och interferometrar.
- Fångade jonkvantdatorer: Laddade atomer används som qubits. Atomerna joniseras med en saknad elektron. Det tvånivåtillstånd som kodar qubiten är atomens specifika energinivåer, som kan manipuleras eller mätas med mikrovågor eller laserstrålar.
- Color Center- eller Nitrogen Vacancy-kvantdatorer: Qubits är gjorda av atomer inbäddade i material som kväve i diamant eller kiselkarbid. De skapas med hjälp av kärnspinnet hos de inbäddade atomerna och är sammanflätade med elektroner.
- Neutrala atomer i optiska gitter: Här fångas neutrala atomer i ett optiskt gitter. Det är ett nätverk av laserstrålar. Tvånivåsystemet för qubitarna kan vara atomens hyperfina energinivå eller exciterade tillstånd.
Dessa är några av de viktigaste tillvägagångssätten för att bygga kvantdatorer. Alla har sina egna unika egenskaper och utmaningar. Kvantberäkning utvecklas snabbt. Valet av rätt tillvägagångssätt är avgörande för framtida framgång.
Användningsområden för kvantdatorer
- Kvantsimulering: Kvantdatorer har potential att simulera komplexa kvantsystem. Det gör det möjligt att studera kemiska reaktioner, elektroners beteende i material och olika fysikaliska parametrar. Detta har tillämpningar för att förbättra solpaneler, batterier, läkemedelsutveckling, flygmaterial med mera.
- Kvantalgoritmer: Algoritmer som Shors algoritm och Grovers algoritm kan lösa problem som klassiska datorer har svårt med. Dessa har tillämpningar inom kryptografi, optimering av komplexa system, maskininlärning och AI.
- Cybersäkerhet: Kvantdatorer utgör ett hot mot klassiska krypteringssystem. Men de kan även bidra till cybersäkerhet genom utveckling av kvantresistenta krypteringssystem. Kvantkryptografi, ett område relaterat till kvantberäkning, kan förbättra säkerheten.
- Optimeringsproblem: Kvantdatorer kan hantera komplexa optimeringsproblem mer effektivt än klassiska datorer. Det har tillämpningar i olika branscher, från leveranskedjehantering till finansiell modellering.
- Väderprognoser och klimatförändringar: Även om det inte beskrivs detaljerat i texten, kan kvantdatorer potentiellt förbättra väderprognosmodeller och hjälpa till att hantera klimatrelaterade utmaningar. Detta är ett område som kan dra nytta av kvantberäkning i framtiden.
- Kvantkryptering: Kvantkryptografi ökar datasäkerheten genom att använda kvantprinciper för säker kommunikation. I en tid av växande cyberhot är detta avgörande.
Det är viktigt att vara försiktig med den hype som finns kring kvantdatorer. Många påståenden om deras kapacitet kommer från personer som aktivt samlar in pengar för att utveckla dem.
Historiskt sett har människor inte varit bra på att förutsäga exakt vad nya teknologier ska användas till. Det var till exempel ingen som kunde föreställa sig internet eller allt det innebar när de första datorerna uppfanns. Samma sak kommer troligtvis att hända med kvantdatorer.
Slutgiltiga tankar
Kvantdatorer blir bättre för varje dag, och även om vi inte kan använda dem i våra dagliga liv ännu, har de potential för praktiska tillämpningar i framtiden.
Den här texten har beskrivit olika aspekter av kvantdatorer. Bland annat har grundläggande koncept som superposition, sammanflätning och interferens förklarats.
Kvantalgoritmer, inklusive Shors algoritm och Grovers algoritm, har diskuterats. Kvantkomplexitetsteori och de olika modellerna för kvantdatorer har också behandlats.
Utmaningarna och de praktiska aspekterna av kvantberäkning har också gåtts igenom. Slutligen har ett stort urval av potentiella användningsområden för kvantdatorer presenterats.
Därefter kan du läsa om vanliga frågor om kvantberäkning.