Sortering är en av de mest använda funktionerna inom programmering. Och det kommer att ta tid att slutföra sorteringen om vi inte använde rätt algoritm.
I den här artikeln kommer vi att diskutera olika sorteringsalgoritmer.
Vi kommer att gå igenom de olika sorteringsalgoritmerna med varje steg som kommer i implementeringen. Implementeringsdelen kommer att vara i Python. Du kan enkelt konvertera den till valfritt språk när du har fått algoritmen. Det är frågan om språksyntax.
Vi kommer att se olika algoritmer från sämsta till bästa i denna handledning. Så, oroa dig inte. Följ artikeln och implementera dem.
Låt oss dyka in i sorteringsalgoritmerna.
Innehållsförteckning
Insättningssortering
Insättningssortering är en av de enkla sorteringsalgoritmerna. Det är lätt att implementera. Och det kommer att kosta dig mer tid att sortera en array. Den kommer inte att användas i de flesta fall för sortering för större arrayer.
Insättningssorteringsalgoritmen upprätthåller sorterade och osorterade underdelar i den givna arrayen.
Den sorterade underdelen innehåller endast det första elementet i början av sorteringsprocessen. Vi tar ett element från den osorterade arrayen och placerar dem på rätt plats i den sorterade underarrayen.
Låt oss se de visuella illustrationerna av infogning sortera steg för steg med ett exempel.
Låt oss se stegen för att implementera infogningssorteringen.
- Initiera arrayen med dummydata (heltal).
- Iterera över den givna arrayen från det andra elementet.
- Ta den aktuella positionen och elementet i två variabler.
- Skriv en slinga som itererar tills det första elementet i arrayen eller elementet inträffar som är mindre än det aktuella elementet.
- Uppdatera det aktuella elementet med det föregående elementet.
- Minska den aktuella positionen.
- Här måste slingan nå antingen början av arrayen eller hitta ett mindre element än det aktuella elementet. Byt ut det aktuella positionselementet med det aktuella elementet.
Tidskomplexiteten för infogningssorteringen är O(n^2), och rymdkomplexiteten om O(1).
Det är allt; vi har sorterat den givna arrayen. Låt oss köra följande kod. Jag hoppas att du har installerat Python, om inte, kolla in installationsguiden. Alternativt kan du använda en online Python-kompilator.
def insertion_sort(arr, n): for i in range(1, n): ## current position and element current_position = i current_element = arr[i] ## iteratin until ### it reaches the first element or ### the current element is smaller than the previous element while current_position > 0 and current_element < arr[current_position - 1]: ## updating the current element with previous element arr[current_position] = arr[current_position - 1] ## moving to the previous position current_position -= 1 ## updating the current position element arr[current_position] = current_element if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] insertion_sort(arr, 9) ## printing the array print(str(arr))
Urval Sortera
Urvalssorteringen liknar insättningssorteringen med en liten skillnad. Denna algoritm delar också upp arrayen i sorterade och osorterade underdelar. Och sedan, vid varje iteration, tar vi minimielementet från den osorterade underdelen och placerar den i den sista positionen i den sorterade underdelen.
Låt oss illustrationer av urval sortera för bättre förståelse.
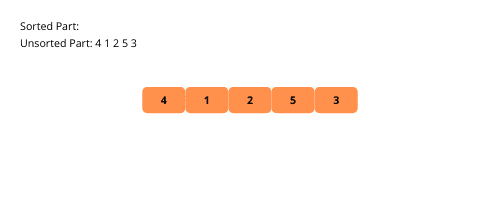
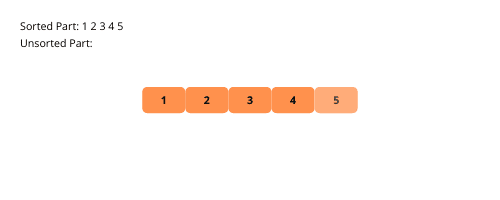
Låt oss se stegen för att implementera urvalssorteringen.
- Initiera arrayen med dummydata (heltal).
- Iterera över den givna arrayen.
- Behåll indexet för minimielementet.
- Skriv en slinga som itererar från det aktuella elementet till det sista elementet.
- Kontrollera om det aktuella elementet är mindre än minimielementet eller inte.
- Om det aktuella elementet är mindre än minimielementet, ersätt sedan indexet.
- Vi har minsta elementindex med oss. Byt ut det aktuella elementet med minimielementet med hjälp av indexen.
Tidskomplexiteten för urvalssorteringen är O(n^2), och rymdkomplexiteten om O(1).
Försök att implementera algoritmen eftersom den liknar insättningssorteringen. Du kan se koden nedan.
def selection_sort(arr, n): for i in range(n): ## to store the index of the minimum element min_element_index = i for j in range(i + 1, n): ## checking and replacing the minimum element index if arr[j] < arr[min_element_index]: min_element_index = j ## swaping the current element with minimum element arr[i], arr[min_element_index] = arr[min_element_index], arr[i] if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] selection_sort(arr, 9) ## printing the array print(str(arr))
Bubblesort
Bubblesortering är en enkel algoritm. Den byter ut de intilliggande elementen på varje iteration upprepade gånger tills den givna matrisen är sorterad.
Den itererar över matrisen och flyttar det aktuella elementet till nästa position tills det är mindre än nästa element.
Illustrationer hjälper oss att förstå bubbelsorteringen visuellt. Låt oss se dem.
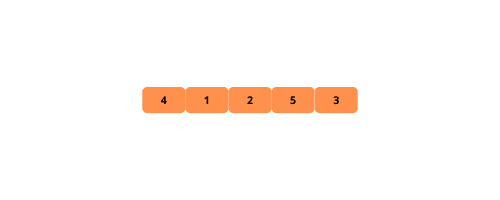
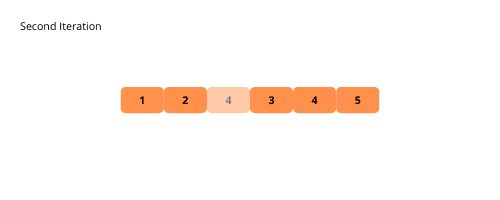
Låt oss se stegen för att implementera bubbelsortering.
Tidskomplexiteten för bubbelsorteringen är O(n^2), och rymdkomplexiteten om O(1).
Du kan enkelt implementera bubblesorteringen nu. Låt oss se koden.
def bubble_sort(arr, n): for i in range(n): ## iterating from 0 to n-i-1 as last i elements are already sorted for j in range(n - i - 1): ## checking the next element if arr[j] > arr[j + 1]: ## swapping the adjucent elements arr[j], arr[j + 1] = arr[j + 1], arr[j] if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] bubble_sort(arr, 9) ## printing the array print(str(arr))
Sammanfoga sortering
Merge sort är en rekursiv algoritm för att sortera den givna matrisen. Det är mer effektivt än de tidigare diskuterade algoritmerna när det gäller tidskomplexitet. Den följer uppdelningen och erövrar-metoden.
Algoritmen för sammanslagningssortering delar upp arrayen i två halvor och sorterar dem separat. Efter att ha sorterat de två halvorna av arrayen slår den samman dem till en enda sorterad array.
Eftersom det är en rekursiv algoritm delar den upp arrayen tills arrayen blir den enklaste (array med ett element) att sortera.
Det är dags för illustration. Låt oss se det.
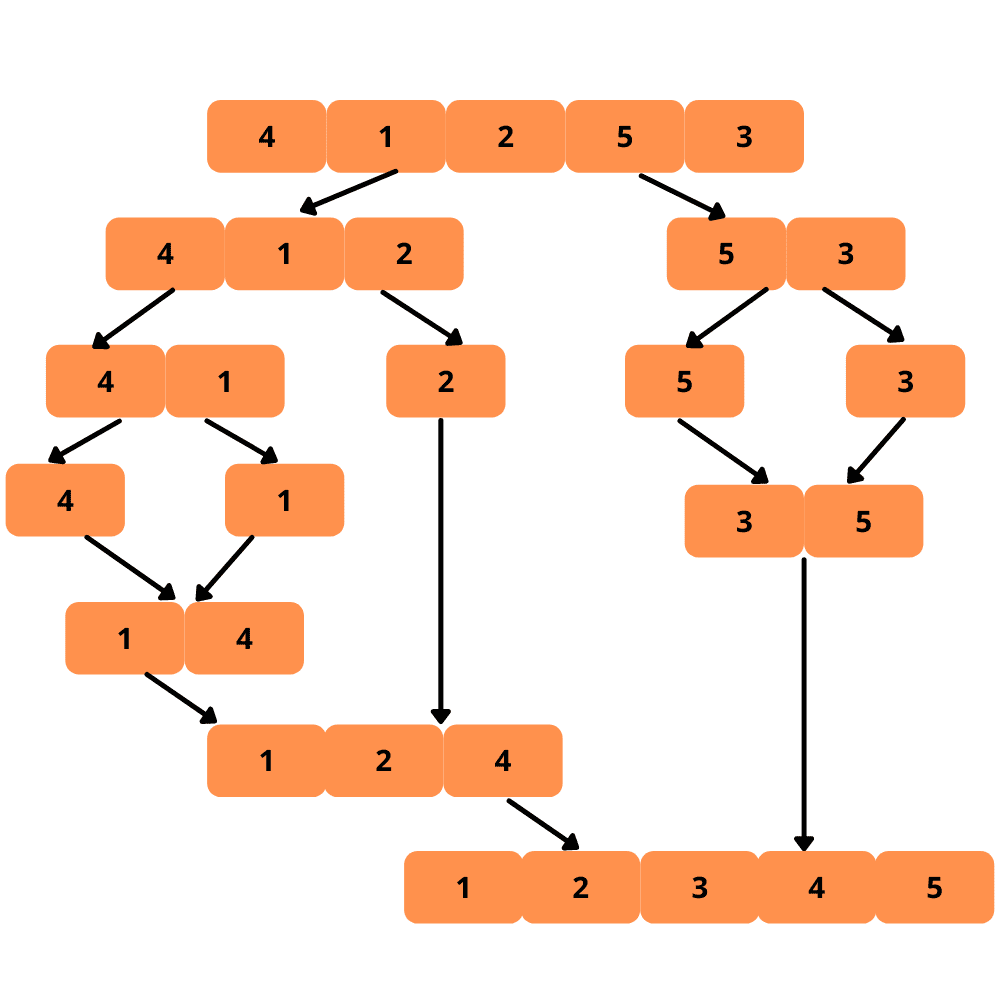
Låt oss se stegen för att implementera sammanslagningssorteringen.
- Initiera arrayen med dummydata (heltal).
- Skriv en funktion som heter merge för att slå samman sub-arrays till en enda sorterad array. Den accepterar argumenten array, left, mid och right index.
- Få längden på vänster och höger sub-arrays längder med hjälp av de givna indexen.
- Kopiera elementen från arrayen till respektive vänster och höger array.
- Iterera över de två sub-arrayerna.
- Jämför de två sub-arrayelementen.
- Byt ut arrayelementet med det mindre elementet från de två underarrayerna för sortering.
- Kontrollera om några element finns kvar i båda sub-arrayerna.
- Lägg till dem i arrayen.
- Skriv en funktion som heter merge_sort med parametrar array, left och right index.
- Om det vänstra indexet är större än eller lika med det högra indexet, återvänd sedan.
- Hitta mittpunkten i arrayen för att dela arrayen i två halvor.
- Anrop merge_sort rekursivt med hjälp av vänster-, höger- och mittindex.
- Efter de rekursiva anropen, slå samman matrisen med sammanfogningsfunktionen.
Tidskomplexiteten för sammanslagningssorteringen är O(nlogn), och rymdkomplexiteten om O(1).
Det var allt för implementeringen av merge sort algoritmen. Kontrollera koden nedan.
def merge(arr, left_index, mid_index, right_index): ## left and right arrays left_array = arr[left_index:mid_index+1] right_array = arr[mid_index+1:right_index+1] ## getting the left and right array lengths left_array_length = mid_index - left_index + 1 right_array_length = right_index - mid_index ## indexes for merging two arrays i = j = 0 ## index for array elements replacement k = left_index ## iterating over the two sub-arrays while i < left_array_length and j < right_array_length: ## comapring the elements from left and right arrays if left_array[i] < right_array[j]: arr[k] = left_array[i] i += 1 else: arr[k] = right_array[j] j += 1 k += 1 ## adding remaining elements from the left and right arrays while i < left_array_length: arr[k] = left_array[i] i += 1 k += 1 while j < right_array_length: j += 1 k += 1 def merge_sort(arr, left_index, right_index): ## base case for recursive function if left_index >= right_index: return ## finding the middle index mid_index = (left_index + right_index) // 2 ## recursive calls merge_sort(arr, left_index, mid_index) merge_sort(arr, mid_index + 1, right_index) ## merging the two sub-arrays merge(arr, left_index, mid_index, right_index) if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] merge_sort(arr, 0, 8) ## printing the array print(str(arr))
Slutsats
Det finns många andra sorteringsalgoritmer, men ovan är några av de ofta använda. Hoppas du tyckte om att lära dig sorteringen.
Ta sedan reda på mer om sökalgoritmer.
Glad kodning 🙂 👨💻