Vad är Procentuellt Fel?
Procentuellt fel, ett mått på noggrannhet, representerar avvikelsen mellan ett uppmätt eller beräknat värde och det sanna eller accepterade värdet. Denna avvikelse uttrycks som en procentandel av det sanna värdet, vilket innebär att resultatet multipliceras med 100. Detta ger en tydlig bild av hur stor felmarginalen är i förhållande till det ursprungliga värdet.
Procentuellt fel kan presenteras som antingen absolut eller relativt fel. Fel kan uppstå på grund av olika faktorer, till exempel maskinernas precision, felberäkningar, mätosäkerheter eller yttre miljöpåverkan. Det är ett vanligt fenomen i både vetenskapliga experiment och praktiska tillämpningar.
Att förstå procentuella fel är avgörande för att bedöma hur pålitliga våra resultat är. Mindre procentuella fel tyder på att våra uppmätta värden är nära det sanna värdet, medan större fel indikerar en signifikant avvikelse. Det är viktigt att kunna tolka dessa fel för att kunna dra korrekta slutsatser och fatta välgrundade beslut.
Ett litet procentuellt fel, låt oss säga 2%, signalerar att vi har en god överensstämmelse med det faktiska värdet. Ett mycket högt fel, som 56%, avslöjar en betydande diskrepans mellan det uppmätta och det sanna värdet. Detta illustrerar hur viktigt det är att analysera procentuella fel för att validera data.
Mätfel är oundvikliga. Det kan bero på faktorer som darrande händer, instrumentens kalibrering, materialens precision och andra oförutsedda omständigheter. Att erkänna och hantera dessa fel är en viktig del av vetenskapliga metoder.
Hur Beräknar Man Procentuellt Fel?
För att beräkna procentuellt fel behöver du två grundläggande värden: det sanna värdet och det uppmätta eller beräknade värdet. Beräkningen inleds med att subtrahera det uppmätta värdet från det sanna värdet. Detta resultat divideras sedan med det sanna värdet. Slutligen multipliceras kvoten med 100 för att uttrycka felet som en procentandel. I grunden är procentuellt fel ett relativt fel multiplicerat med 100.
Formeln för att beräkna procentuellt fel är:
Procentuellt fel = [(Sanningens värde – Uppmätt värde) / Sanningens värde] × 100
Formelns Komponenter
Sanningens värde: Detta är det numeriska värde som anses vara den exakta eller mest korrekta representationen av det vi mäter. Det är det idealiska värdet som vi strävar efter att uppnå i våra mätningar.
Uppmätt värde: Det uppmätta värdet är det resultat som erhålls från ett experiment eller en mätning. Ofta avviker det från sanningens värde på grund av de felkällor som nämnts tidigare, såsom maskinens precision, fel vid avläsningen eller omgivningens påverkan.
Exempel på Beräkningar
Exempel 1
En pojke mäter arean på en triangel och får resultatet 462 kvadratmeter. Det faktiska värdet för triangelns area är 465 kvadratmeter. Vi ska beräkna det procentuella felet i pojkens mätning.
Lösning:
Uppmätt area = 462 kvm
Verklig area = 465 kvm
Beräkning:
Skillnad mellan verkligt värde och uppmätt värde: 465 – 462 = 3
Felet är 3 kvadratmeter.
Dividera felet med det faktiska värdet: 3 / 465 = 0,00645
Multiplicera med 100 för att få procentuellt fel: 0,00645 * 100 = 0,64 %
Det procentuella felet i pojkens mätning är 0,64 %.
Exempel 2
Du planerar en fest och räknar med att 20 personer kommer. Endast 18 personer dyker upp. Beräkna procentfelet i din uppskattning.
Lösning:
Förväntat antal gäster = 20
Antal gäster som kom = 18
Beräkning:
Skillnad mellan förväntat och faktiskt antal gäster: 20 – 18 = 2
Felet är 2 personer.
Dividera felet med det faktiska värdet: 2 / 20 = 0,1
Multiplicera med 100 för att få procentuellt fel: 0,1 * 100 = 10 %
Procentfelet i din gästuppskattning är 10 %.
Exempel 3
Du mäter vattnets kokpunkt i ett experiment. Ditt resultat visar 102°C. Den faktiska kokpunkten för vatten är 100°C. Beräkna procentfelet i din mätning.
Lösning:
Faktisk kokpunkt för vatten = 100°C
Uppmätnings kokpunkt för vatten = 102°C
Beräkning:
Skillnaden mellan uppmätt och faktiskt värde: 100 – 102 = -2 (vi tar absoluta värdet = 2)
Felet är 2°C
Dividera felet med det faktiska värdet: 2 / 100 = 0,02
Multiplicera med 100 för att få procentuellt fel: 0,02 * 100 = 2 %
Det procentuella felet i mätningen av vattnets kokpunkt är 2 %.
När är Procentuellt Fel Viktigt?
- Procentuellt fel är ett ovärderligt verktyg för att utvärdera noggrannheten i utförda uppgifter och för att identifiera fel som begåtts under processen.
- Det är särskilt viktigt inom vetenskapliga laboratorier och industrier där minsta fel kan få betydande konsekvenser.
- Procentuella fel används också vid massproduktion där det är avgörande att minimera felmarginalerna.
- Inom vetenskaplig forskning är noggrannheten i mätningar och beräkningar av yttersta vikt, och procentuella fel är ett viktigt verktyg för att uppnå denna precision.
Procentuellt Fel kontra Absolut Fel
Absolut fel representerar skillnaden mellan ett uppmätt värde och det sanna värdet. Det absoluta felet har samma enhet som den mätning som gjorts.
Till exempel, om du beställer 2 kg mango och du får 1,98 kg, då är det absoluta felet 2 – 1,98 = 0,02 kg.
Procentuellt fel, å andra sidan, beräknas genom att dividera det absoluta felet med det faktiska värdet och sedan multiplicera resultatet med 100. Procentuellt fel är enhetslöst och uttrycks i procent.
I det tidigare exemplet med mango var det absoluta felet 0,02 kg. För att beräkna procentfelet dividerar vi 0,02 med 2 (det sanna värdet) och får 0,01. Multiplicerat med 100, blir det procentuella felet 0,1%.
Procentuellt Fel kontra Relativt Fel
Relativt fel är det absoluta felet dividerat med det sanna värdet. Det procentuella felet är i praktiken samma sak som det relativa felet, men det är multiplicerat med 100 och uttrycks i procent.
Låt oss ta ett exempel: En väderprognos lovar 38°C, men temperaturen stiger till 42°C.
Först räknar vi ut skillnaden mellan det förväntade och det faktiska värdet: 42 – 38 = 4°C
För att räkna ut det relativa felet delar vi skillnaden med det sanna värdet: 4 / 38 = 0,1052.
Procentuellt fel är det relativa felet multiplicerat med 100. I detta fall blir procentfelet 0,1052 * 100 = 10,52 %.
Att beräkna dessa olika typer av fel kan initialt verka svårt, men det är relativt enkelt när man har förstått formlerna och sammanhanget.
För att underlätta beräkningarna finns det även flera onlineverktyg tillgängliga som kan räkna ut procentuellt fel automatiskt.
Verktyg för Felberäkning
#1. Calculator Soup
Calculator Soup är en användarvänlig räknare som beräknar procentuellt fel baserat på det experimentella och faktiska värdet. Användaren behöver bara ange de relevanta värdena för att få ett omedelbart och exakt resultat.
Sidan är uppbyggd med tydliga kolumner där de värden som ska användas i beräkningen anges. Räknaren sköter sedan resten av beräkningarna automatiskt.
#2. Calculator.net
Calculator.net erbjuder också en praktisk lösning för att beräkna procentuella fel. Med bara två indatafält, ett för det sanna värdet och ett för det uppmätta värdet, kan användaren snabbt få svaret. Detta verktyg är särskilt användbart när det finns stora mängder data att hantera och där manuella beräkningar är tidskrävande.
Det är viktigt att notera att procentuella fel är svåra att eliminera helt. Vi kan försöka minimera dem, men det är nästintill omöjligt att få ett procentuellt fel på exakt noll.
#3. Good Calculators
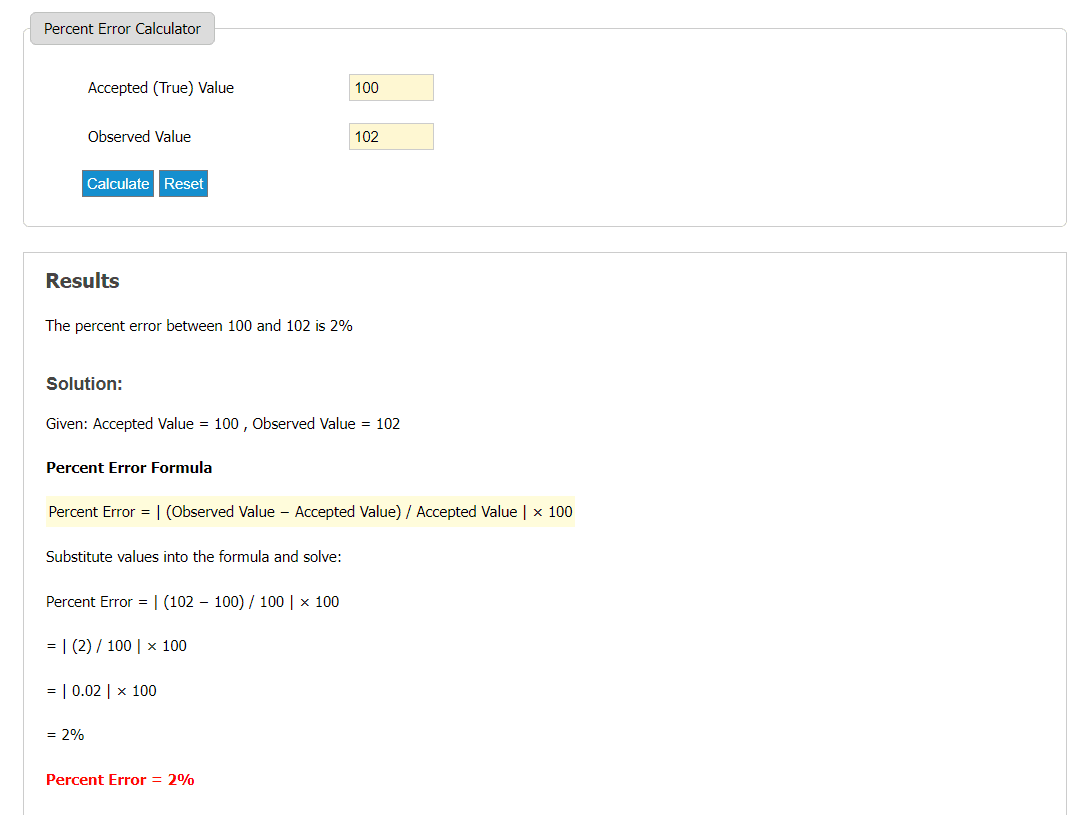
En annan onlinekalkylator som är värd att nämna är Good Calculators. Användaren anger helt enkelt de förväntade och faktiska värdena, och resultatet beräknas automatiskt.
Detta verktyg är tidseffektivt och sparar användaren från de traditionella manuella beräkningarna. Det är särskilt fördelaktigt i situationer där snabba och korrekta beräkningar krävs.
Dessa onlineverktyg är utmärkta resurser för snabb och noggrann beräkning av procentuella fel, särskilt när du har omfattande datamängder att hantera men ont om tid.
Sammanfattning
Fel i beräkningar kan äventyra ett projekt. För att minimera riskerna är det viktigt att använda noggranna metoder för felberäkning. Att dra nytta av online-räknare är ett sätt att säkerställa att arbetet blir så effektivt och felfritt som möjligt.
För de som är intresserade av ekonomi kan det vara av intresse att titta på olika kalkylatorer för vinstmarginaler.