För att lyckas med sina finansiella ambitioner är noggrann planering a och o. Oavsett om man siktar på att spara pengar till ett framtida köp eller hantera befintliga lån kan det vara svårt att exakt beräkna den tid som krävs för att nå sina mål.
Det är här Excels NPER-funktion blir ett ovärderligt verktyg. Denna funktion tar hänsyn till diverse variabler såsom räntesatser och betalningsbelopp för att ge dig den finansiella prognos du behöver. Låt oss utforska grunderna och detaljerna i NPER-funktionen så att du kan fatta välgrundade ekonomiska beslut.
Vad är NPER-funktionen i Excel?
NPER är en av Excels finansiella funktioner som är avsedd för att hjälpa dig göra korrekta ekonomiska beräkningar. NPER står för ”Number of Periods”, vilket refererar till det antal betalningsperioder som krävs för att uppnå ett visst ekonomiskt mål. Funktionen utgår från regelbundna betalningar till en konstant ränta.
NPER-funktionen tar flera parametrar och dess syntax ser ut så här:
=NPER(RÄNTA; BETALNING; NUVP; [SLUTV]; [TYP])
- RÄNTA: Räntesatsen för varje period, angiven i procent.
- BETALNING: Det konstanta betalningsbelopp som erläggs under varje period.
- NUVP (Nuvärde): Det initiala eller aktuella beloppet för investeringen eller lånet.
- SLUTV (Slutvärde): Det önskade framtida värdet på investeringen eller lånet. Denna parameter är valfri.
- TYP: Anger om betalningar görs i början (1) eller slutet (0) av varje period. Denna parameter är också valfri.
Om parametrarna SLUTV och TYP lämnas tomma, sätts de automatiskt till noll. Då de flesta banker beräknar ränta i slutet av varje betalningsperiod, lämnas parametern TYP vanligtvis tom. Värdet som anges för SLUTV beror på sammanhanget, vilket vi ska fördjupa oss i lite senare.
Utöver TYP har var och en av parametrarna i NPER-funktionen en specifik roll som kan hjälpa dig att lösa praktiska ekonomiska problem i Excel.
Förstå NPER-funktionen i Excel
I grund och botten hjälper NPER-funktionen dig att avgöra hur många betalningar som krävs för att uppnå ett visst ekonomiskt mål. Detta kan handla om alla möjliga scenarier, från att spara till semestern, betala av ett bolån, eller planera för pension.
För att använda denna funktion på ett korrekt sätt måste du förstå två centrala begrepp: kassaflöde och betalningsintervall.
Kassaflöde
Det finns tre kassaflödesparametrar i NPER-funktionen: betalningen som görs varje period, nuvärdet och det framtida värdet. Det är viktigt att notera att dessa värden inte alla är positiva.
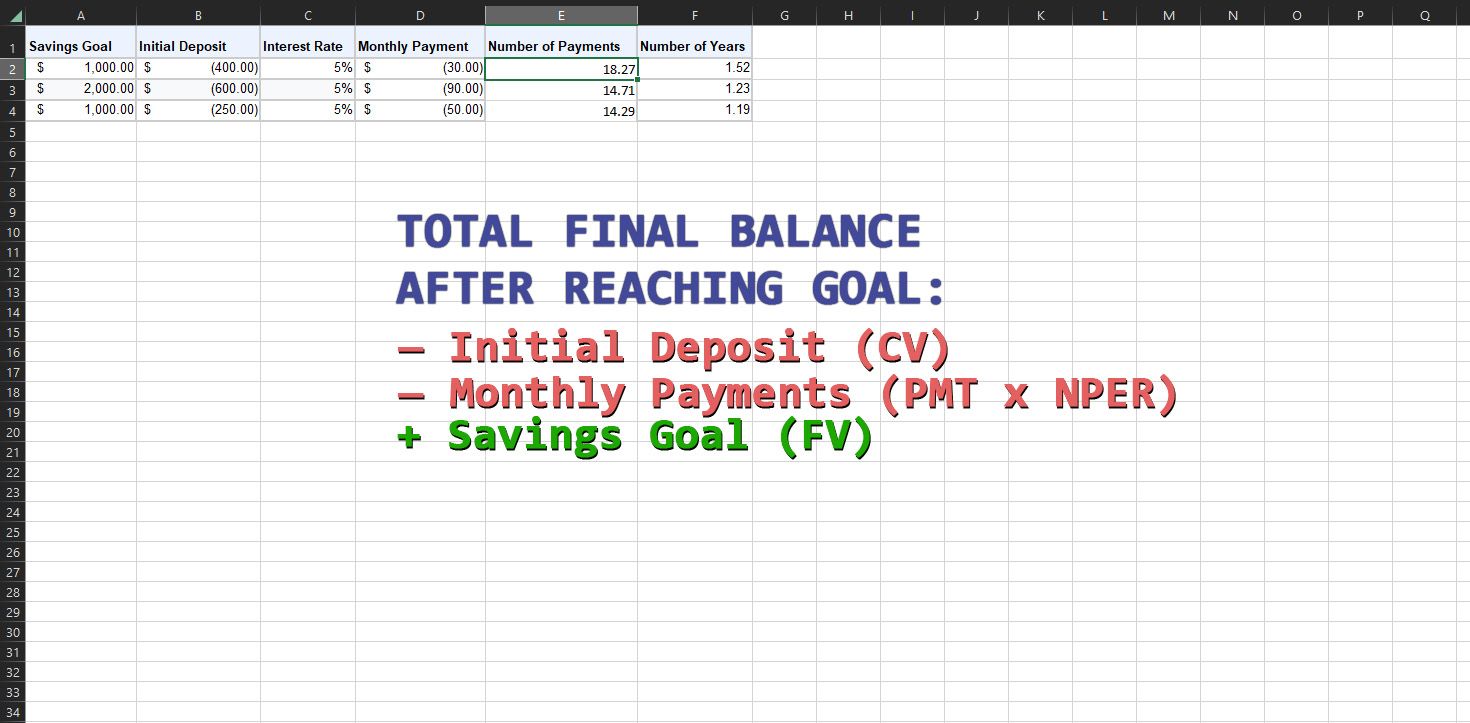
När det gäller ett sparkonto, är betalningarna som görs varje period (BETALNING) och den initiala insättningen (NUVP) utgifter. Å andra sidan, är det framtida värdet på sparkontot (SLUTV) en inkomst. Du betalar ut BETALNING och NUVP från din egen ficka för att få SLUTV på sparkontot. Därför bör BETALNING och NUVP anges som negativa värden.
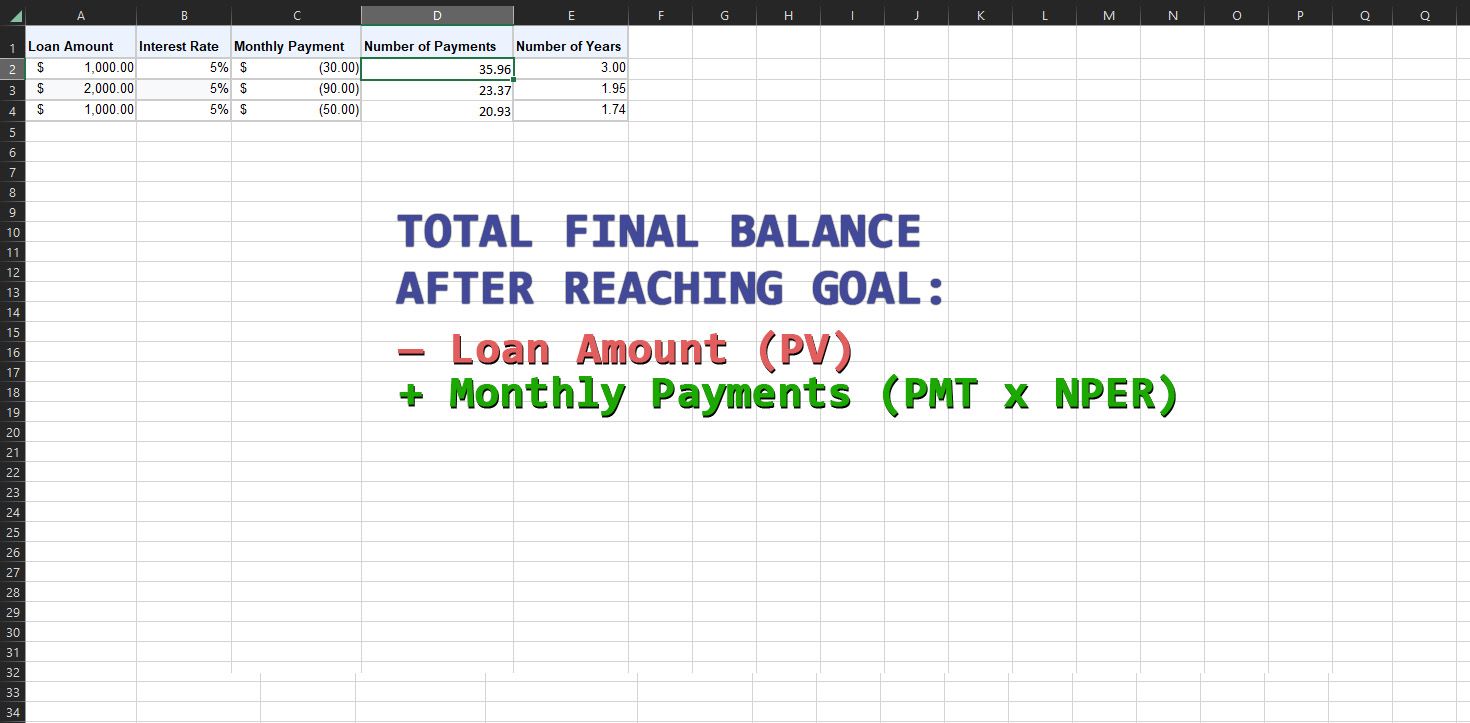
Det motsatta gäller för lån. För ett lån är BETALNING positiv, NUVP negativ och SLUTV noll. Föreställ dig ett bankkonto med lånebeloppet som nuvärde. I det fallet är du skyldig banken pengar och måste betala tillbaka lånet med ränta. Du gör månatliga betalningar till bankens konto och slutar betala när skuldbeloppet når noll.
Betalningen som görs varje månad (BETALNING) är det belopp som du bidrar med till det negativa NUVP för att nå noll. Därför ska värdena för BETALNING vara positiva. Om du inte betalar tillbaka lånet du fått från banken (NUVP), kommer det fortsätta att öka, vilket resulterar i ett större negativt tal.
Betalningsintervall
En annan viktig faktor att tänka på när man använder NPER är betalningsintervallet. För både lån och sparkonton, får den ena parten mer än vad den gav, på den andra partens bekostnad. Det finns två betalningsintervall att ta hänsyn till här: ränteperioden och betalningsperioden.
Ränteperioden hänvisar till det intervall med vilket banken tillämpar ränta på lånet eller betalar ränta på ditt sparande. Detta är vanligtvis varje månad, men kan även vara årligen. Om en bank säger att de ger dig en ränta på 12 % på dina besparingar och de lägger till denna ränta en gång om året, i slutet av året, får du 12 % extra av din ursprungliga insättning.
Men om de säger att det är 12 % årlig ränta och de lägger till lite varje månad, delar de inte bara de 12 % med 12 månader och ger dig 1 % varje månad. När banken lägger till lite ränta varje månad börjar räntan också tjäna in sin egen ränta (det kallas sammansatt ränta). Så i slutet av året tjänar du något mer än 12 %, närmare bestämt 12,68 %.
Även om skillnaden verkar försumbar kan den göra en väsentlig skillnad med större kapitalbelopp över längre tidsperioder.
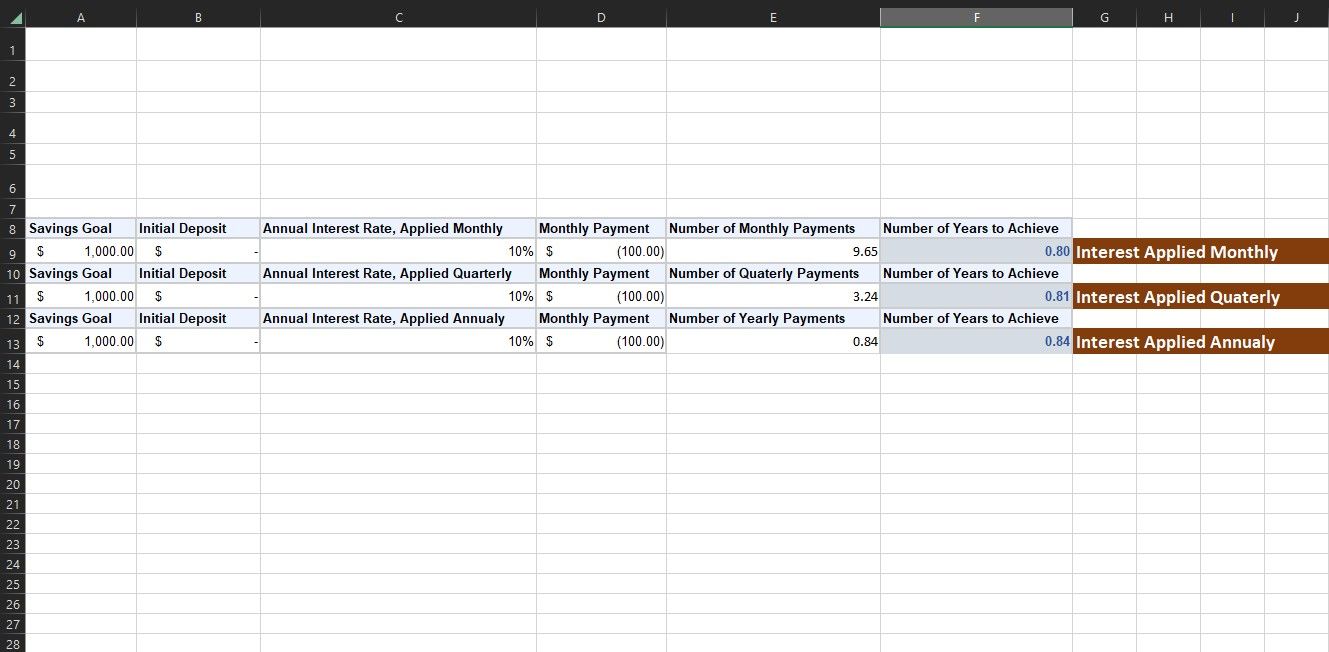
Betalningsperioden syftar på frekvensen med vilken du antingen betalar tillbaka de lånade pengarna eller sätter in ytterligare pengar på ditt sparande. NPER-funktionens utdata är relaterat till betalningsperioden i BETALNING. Om värdet du anger i BETALNING betalas månadsvis, är utdata från NPER i månader. Om värdet du anger är årligen, är utdata i år.
Betalningsperioden går hand i hand med det vi diskuterat om ränteperioden. Frekvensen du väljer för betalningsperioden ska motsvara frekvensen för den ränta du har att göra med. Så om räntan tillämpas månadsvis, måste du ange det månatliga betalningsbeloppet som BETALNING. Annars blir inte NPER-resultatet korrekt.
Praktiska exempel på användning av NPER-funktionen i Excel
NPER-funktionen är användbar i en rad olika verkliga scenarier. Med en korrekt förståelse av betalningsintervall och kassaflöde kan du använda NPER för att beräkna alla typer av ekonomiska mål. Låt oss undersöka två vanliga exempel.
1. Använd NPER för att beräkna sparande
Anta att du vill skapa ett sparkonto inför en semester. Du räknar med att semestern kommer att kosta $1000, och din bank erbjuder en 12% årlig ränta som betalas månadsvis. Hittills har du SLUTV ($1000) och räntesatsen (12%). Låt oss säga att du vill göra en initial insättning på $100 (-NUVP) på kontot och sedan betala in $70 varje månad (-BETALNING).
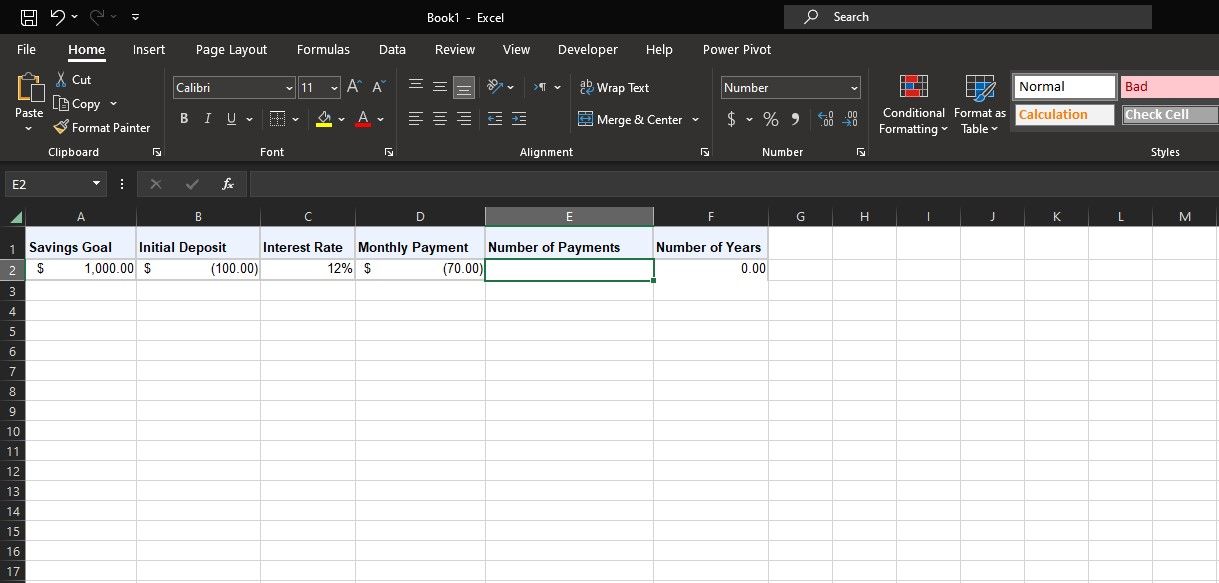
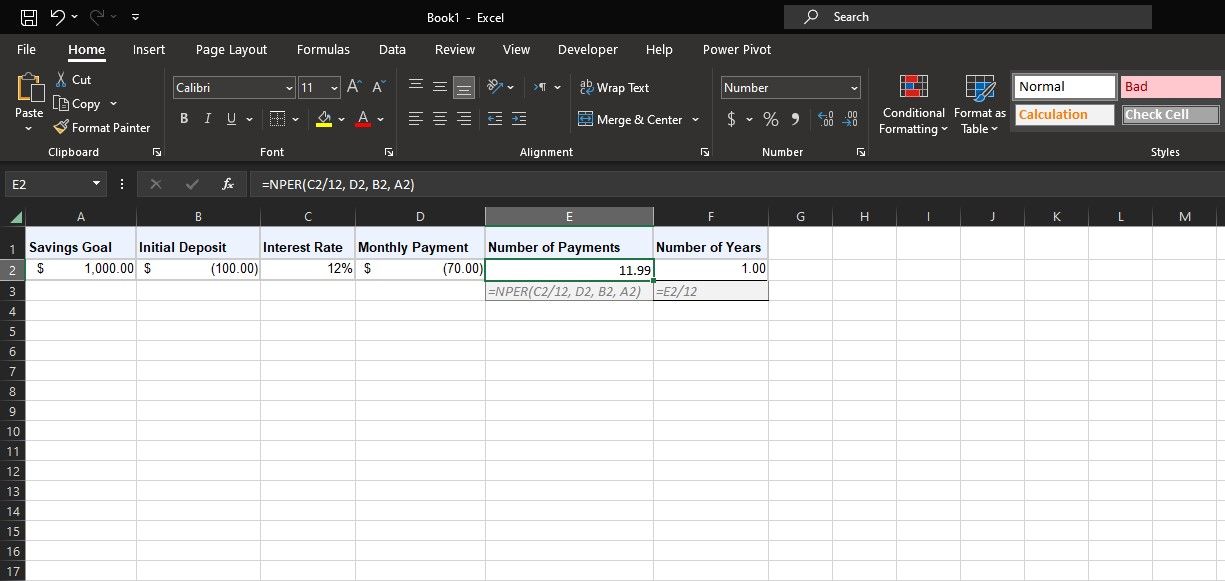
Du kan använda NPER-funktionen för att snabbt beräkna hur lång tid det tar att nå ditt sparmål. Ange värdena i ett kalkylblad som det ovan, och kom ihåg att använda negativa värden för NUVP och BETALNING. Skriv sedan in följande formel för att få antalet betalningar:
=NPER(C2/12; D2; B2; A2)
I den här formeln hänvisar C2 till den årliga räntan. Då räntan tillämpas månadsvis och BETALNING också är månadsvis, delar formeln räntan med 12 för att få månadsräntan. D2 hänvisar till det månatliga betalningsbeloppet (BETALNING). B2 är den initiala insättningen på $100 (NUVP), och A2 är sparmålet (SLUTV).
Alternativt, om du har ett specifikt mål för NPER, kan du använda ”Målsökning” i Excel för att lösa okända variabler, som till exempel den initiala insättningen (NUVP) och de månatliga betalningarna (BETALNING).
2. Använd NPER för att beräkna lån
Excels NPER-funktion är lika användbar vid hantering av lån. Föreställ dig ett scenario där du tar ett billån på $15 000 med en årlig ränta på 16 % som tillämpas varje månad. Du vill hålla dina månatliga betalningar på $300. Med hjälp av NPER-funktionen kan du bestämma hur många månader det tar att betala tillbaka lånet.
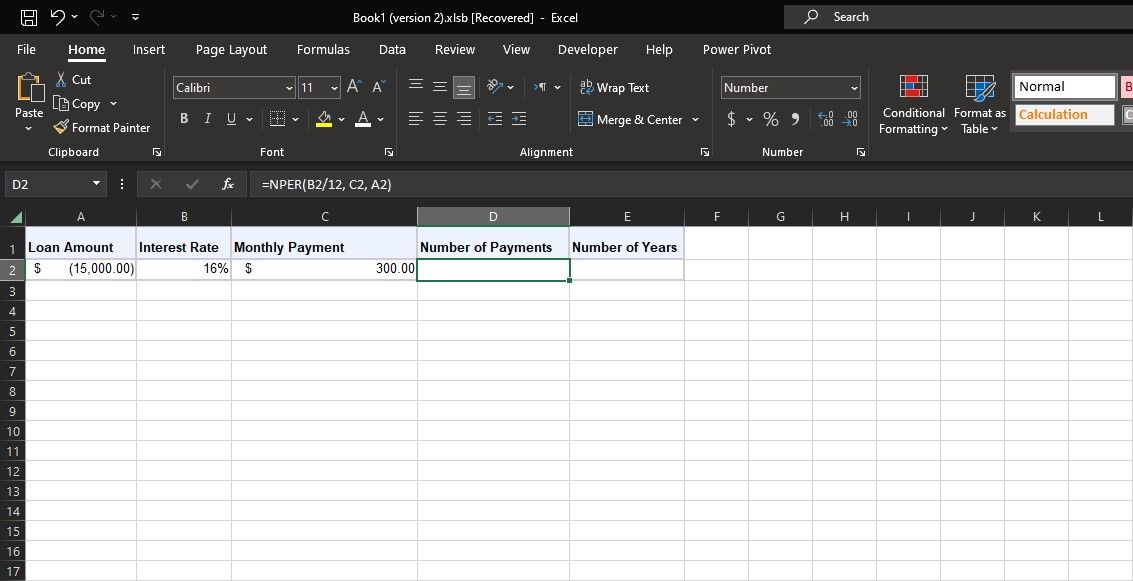
Du har NUVP (-$15 000), räntesats (16 %) och BETALNING ($300). Använd följande NPER-formel för att beräkna antalet betalningar i det här exemplet:
=NPER(B2/12; C2; A2)
I den här formeln hänvisar B2 till den årliga räntan. Eftersom BETALNING är i månader och räntan tillämpas månadsvis, delar formeln detta med 12 för att få månadsräntan. C2 hänvisar till de månatliga betalningarna (BETALNING). A2 är NUVP, vilket är det negativa lånebeloppet. SLUTV lämnas tomt, så formeln antar korrekt att det är noll.
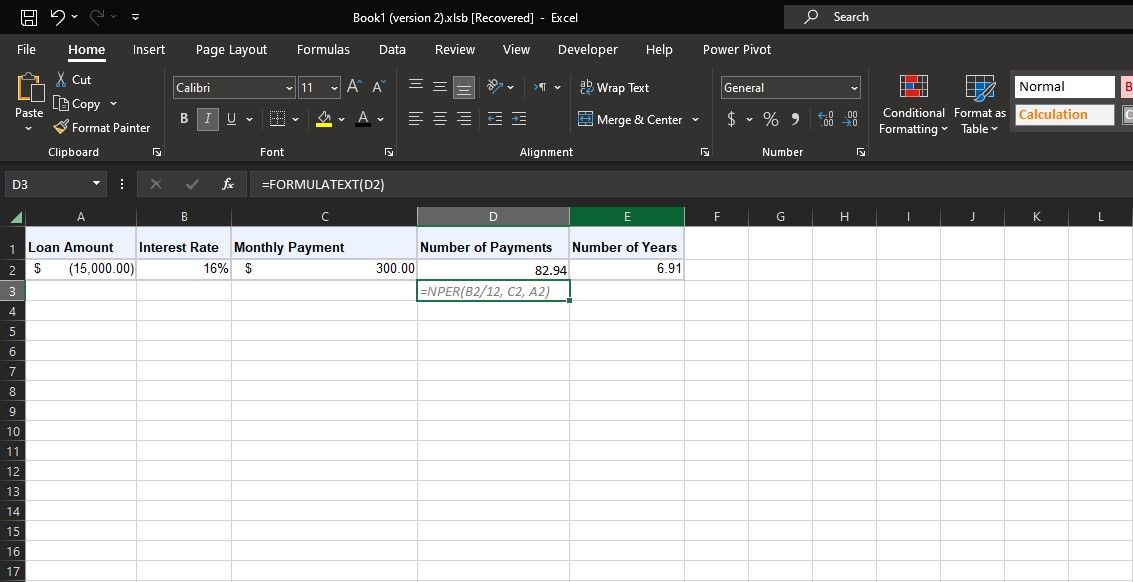
NPER ger 82,94, vilket betyder att det kommer att ta ungefär 83 månader att betala av lånet. Den intilliggande cellen delar detta med 12 och säger att det kommer att ta sju år att betala tillbaka lånet.
Planera dina ekonomiska mål med NPER i Excel
NPER-funktionen i Excel är en värdefull resurs för finansiella prognoser. Genom att låta dig beräkna antalet betalningsperioder som krävs för att nå dina spar- eller lånemål, ger NPER dig möjligheten att ta kontroll över din ekonomiska framtid.
Kom ihåg att även om NPER-funktionen förenklar komplexa beräkningar, är det fortfarande viktigt att kombinera den med gott omdöme och anpassa den till de dynamiska aspekterna av verklig ekonomi.