Betydelsen av sorteringsalgoritmer i programmering
Att ordna listor med data är en grundläggande aspekt inom applikationsutveckling. Det är av stor betydelse för att presentera data på ett strukturerat sätt och underlätta sökoperationer. Därför är det nödvändigt för en kompetent mjukvaruutvecklare att ha kunskap om hur man sorterar arrayer. Denna artikel kommer att beskriva några av de mest använda algoritmerna för att sortera arrayer i JavaScript.
Vad innebär sortering och varför är det värdefullt?
Bildkälla: Unsplash
Sortering handlar om att systematiskt arrangera värden i enlighet med en specifik ordning, antingen stigande eller fallande. Att sortera arrayer i JavaScript är fördelaktigt eftersom det möjliggör en mer meningsfull presentation av data. Till exempel kan användare önska att se filer ordnade efter senast ändrade, eller produkter ordnade efter pris. Det underlättar även binärsökning, en algoritm som endast fungerar på sorterad data.
Trots att det finns inbyggda funktioner och bibliotek som förenklar datorsortering, är det viktigt att förstå sorteringsmekanismerna på en grundläggande nivå. Denna kunskap är användbar för tekniska intervjuer och när man behöver skriva kod på låg nivå.
Sorteringsalgoritmer för JavaScript-arrayer
Bubblesort

Bubblesort är en av de lättaste algoritmerna att förstå och implementera. Den fungerar genom att iterera genom arrayen i flera pass. Under varje pass går vi igenom arrayen från början till slut och jämför intilliggande element. Om elementen är i fel ordning byter vi plats på dem.
Vi utför *n* pass, där *n* är antalet element i arrayen. För varje pass tenderar arrayen att bli mer sorterad, med de största elementen ”bubblar” upp till slutet av arrayen. Här är en pseudokod för att sortera tal i stigande ordning:
1. Låt n vara antalet element i arrayen.
2. Iterera n gånger med variabeln i.
a. Iterera genom arrayen från det andra elementet till element n-i.
b. Om det föregående elementet är större än det nuvarande elementet, byt plats på dem.
I JavaScript skulle den motsvarande koden se ut så här:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
För att få en djupare förståelse för vad som händer, kan det vara hjälpsamt att lägga till console.log() inuti looparna. Detta gör det möjligt att följa arrayens förändring för varje pass. I nedanstående exempel har jag modifierat sort-funktionen med dessa console.log-anrop, samt skapat en osorterad array för att testa funktionen.
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
console.log(`Pass: ${i}`);
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
console.log(arr);
}
}
return arr;
}
const array = [9, 2, 7, 4, 1];
sort(array);
console.log(array);
Utskriften från ovanstående kod skulle se ut som följer:

Bubblesort har en tidskomplexitet på O(n^2), eftersom den genomför n pass genom arrayen för varje pass. Det gör att den inte skalar särskilt bra. Däremot har den en minneskomplexitet på O(1), eftersom den gör ändringar direkt på arrayens element.
Insättningssortering

Insättningssortering är en vanlig algoritm för att sortera arrayer i JavaScript. Anta att vi använder insättningssortering för att sortera tal i stigande ordning. Algoritmen väljer ett tal, som vi kallar `num`. Den flyttar sedan `num` åt vänster tills varje tal till vänster om `num` är mindre än `num`. Denna process upprepas från det andra elementet till slutet av arrayen. Nedan finns en pseudokod beskrivning:
1. Låt n vara antalet element i arrayen
2. Iterera i från 1 till n – 1 (börja från det andra elementet)
a. Sätt `currentElement` till `array[i]`.
b. Sätt j till i – 1.
c. Så länge j >= 0 och `array[j]` > `current_element`
i. Flytta `array[j]` till `array[j+1]`.
ii. Minska j med 1.
d. Sätt `array[j+1]` till `current_element`.
Och här är den motsvarande JavaScript-implementationen:
function insertionSort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
}
return array;
}
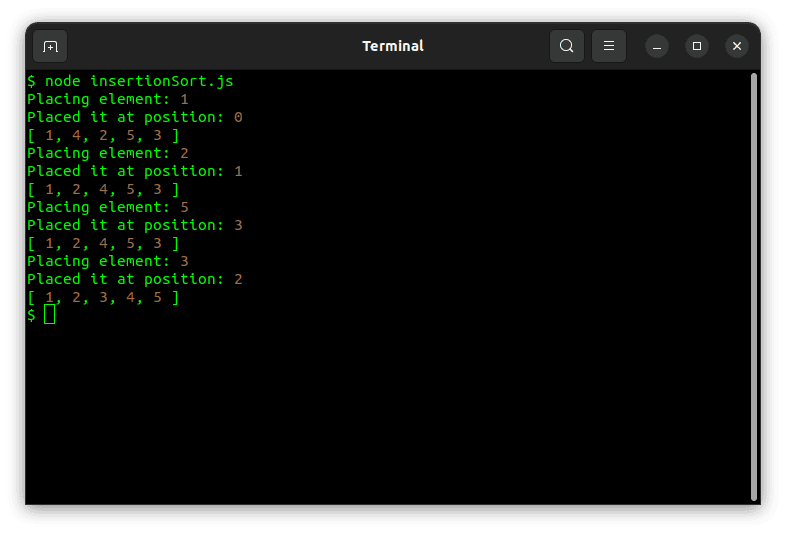
Liksom med Bubblesort kan du använda console.log för att visualisera hur sorteringen fungerar. Kodavsnittet nedan visar insättningssortering i praktiken:
function sort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
console.log("Placing element:", currentElement);
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
console.log("Placed it at position:", j + 1);
console.log(array);
}
return array;
}
const array = [4, 1, 2, 5, 3];
sort(array);
Resultatet av att köra koden ovan är som följer:
Sammanslagningssortering

Medan insättningssortering och bubbelsortering har en kvadratisk tidskomplexitet, skalar sammanslagningssortering med en kvasi-linjär tidskomplexitet av O(n * log(n)).
Sammanslagningssortering använder sig av ”söndra och härska”-strategin. Arrayen delas rekursivt in i mindre arrayer tills varje array endast innehåller ett element. Därefter sammanfogas de mindre arrayerna tillbaka, men på ett sorterat vis.
När arrayerna slås ihop, slås de sorterade delarna samman. Sammanslagningen utförs som när man sammanfogar två sorterade listor. Här följer en pseudokodbeskrivning:
1. Om arrayens längd är 1 eller mindre, returnera arrayen (basfall).
2. Hitta mittenindex:
a. Sätt `mid` till golvet av (längden på arrayen / 2).
3. Dela arrayen i två delarrayer:
a. Skapa `leftArray` och kopiera den första hälften av arrayen till den (från index 0 till `mid`).
b. Skapa `rightArray` och kopiera den andra hälften av arrayen till den (från index `mid+1` till slutet).
4. Anropa rekursivt `MergeSort` på `leftArray`.
5. Anropa rekursivt `MergeSort` på `rightArray`.
6. Sammanfoga de två sorterade delarrayerna:
a. Skapa en tom `resultArray`.
b. Så länge både `leftArray` och `rightArray` inte är tomma:
i. Om det första elementet i `leftArray` är mindre eller lika med det första elementet i `rightArray`, lägg till det i `resultArray`.
ii. Annars, lägg till det första elementet i `rightArray` i `resultArray`.
c. Lägg till eventuella kvarvarande element i `leftArray` i `resultArray` (om det finns några).
d. Lägg till eventuella kvarvarande element i `rightArray` i `resultArray` (om det finns några).
7. Returnera `resultArray`.
Och JavaScript-implementationen ser ut så här:
function sort(array) {
// Base case in which we stop subdividing the array
if (array.length == 1) {
return array;
}
// Finding the middle point of the array
const m = Math.round(array.length / 2);
// Divide the array into two halves
const leftUnsorted = array.slice(0, m);
const rightUnsorted = array.slice(m);
// Recursively call merge sort
const leftSorted = sort(leftUnsorted);
const rightSorted = sort(rightUnsorted);
// Return a merged sorted array
return merge(leftSorted, rightSorted);
}
function merge(left, right) {
// Merge two sorted lists
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex += 1;
} else {
result.push(right[rightIndex]);
rightIndex += 1;
}
}
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
Kör du koden med en testarray borde den fungera som den ska.
Quicksort

Precis som Mergesort bygger Quicksort på ”söndra och härska”-strategin. Algoritmen väljer ett ”pivot”-element. Därefter flyttar den alla element som är större än pivoten till höger om pivoten och alla element som är mindre till vänster. När detta är gjort hamnar pivoten på sin rätta plats.
För att flytta elementen runt pivoten, börjar algoritmen med att flytta pivoten till slutet av arrayen. Därefter används en pekare för att loopa genom arrayen från vänster. Denna pekare letar efter det första talet som är större än pivoten. Samtidigt används en andra pekare från höger, som letar efter det första talet som är mindre än pivoten. När båda talen har identifierats, byts de. Denna process fortsätter tills den vänstra pekaren är större än den högra pekaren.
När processen är klar, byter vi plats på det största av de två senast utbytta talen med pivoten. Nu hamnar pivoten på sin rätta plats, alla tal mindre än pivoten till vänster, och alla tal större än pivoten till höger.
Denna process repeteras rekursivt för delarrayerna till vänster och höger om pivoten, tills delarrayerna bara har ett element.
Här följer en pseudokod för Quicksort:
1. Om `lessThanPointer` är mindre än `greaterThanPointer`:
a. Välj ett pivotelement från arrayen.
b. Flytta element så att de element som är mindre hamnar till vänster och de som är större till höger.
c. Anropa rekursivt `Quicksort` på vänster sub-array.
d. Anropa rekursivt `Quicksort` på höger sub-array.
Och den motsvarande JavaScript koden:
function sort(array, low, high) {
if (low < high) {
// Choose the pivot index and partition the array
const pivotIndex = move(array, low, high);
// Recursively sort the subarrays to the left and right of the pivot
sort(array, low, pivotIndex - 1);
sort(array, pivotIndex + 1, high);
}
}
function move(array, low, high) {
// Select the pivot element (in this case, the last element)
const pivotElement = array[high];
// Initialize the index for the smaller element
let i = low - 1;
for (let j = low; j < high; j++) {
// If the current element is less than or equal to the pivot, swap it with the element at index i+1
if (array[j] <= pivotElement) {
i += 1;
const temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// Swap the pivot element into its correct position
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// Return the index of the pivot element
return i + 1;
}
Om du sorterar en testarray med Quicksort i Node.js, borde resultatet bli följande:
I bästa fall har Quicksort en kvasi-linjär tidskomplexitet. Minnesanvändningen i Quicksort skalar också logaritmiskt. Detta gör den relativt effektiv i jämförelse med andra sorteringsalgoritmer för arrayer i JavaScript.
Tips inför programmeringsintervjuer
❇️ Övning ger färdighet. Genom att öva lär du dig olika algoritmer, och ännu viktigare, det hjälper dig utveckla dina förmågor i problemlösning och beräkningstänkande. Du kan öva på plattformar som Leetcode och AlgoExpert.
❇️ Försök att lösa problemet själv först. Istället för att direkt gå till lösningen, försök att lösa den själv, eftersom det hjälper dig utveckla din problemlösningsförmåga.
❇️ Om ett problem tar för lång tid, hoppa över det och gå direkt till lösningen. Du kan ändå lära dig lösa problemet genom att studera lösningen. De flesta läroplattformar tillhandahåller lösningar. Verktyg som ChatGPT eller Google Bard kan också vara användbara för att förklara begrepp.
❇️ Undvik att skriva kod direkt. Skissa dina lösningar på ett papper, och tänk igenom dem innan du börjar koda. Pseudokod är också ett bra verktyg för att snabbt skriva ner dina tankar.
Slutsats
I denna artikel har vi gått igenom de mest använda sorteringsalgoritmerna. Att lära sig allt detta kan kännas överväldigande i början. Därför brukar jag rekommendera att blanda olika läromedel istället för att bara förlita sig på en källa. Lycka till med programmeringen!
Ta gärna en titt på hur man använder sorteringsfunktioner i Python.