Det finns ofta en viss osäkerhet i statistiska data, även om man noggrant följer alla procedurer och använder avancerad utrustning för mätningar. Lyckligtvis kan Excel hjälpa oss att beräkna denna osäkerhet baserat på standardavvikelsen i våra data.
Excel erbjuder en rad statistiska funktioner som vi kan använda för att kvantifiera osäkerheten. I den här artikeln ska vi undersöka hur man beräknar det aritmetiska medelvärdet, standardavvikelsen och standardfelet. Vi kommer också att visa hur man kan visualisera denna osäkerhet i ett diagram i Excel.
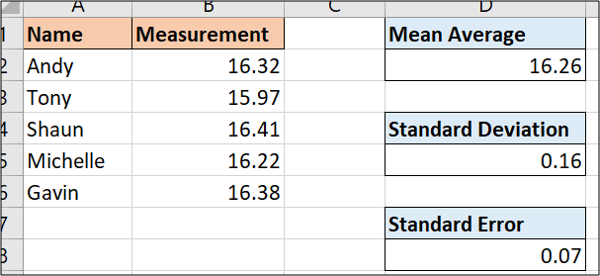
Vi kommer att utgå från följande exempeldata för att demonstrera dessa beräkningar:
Denna data representerar fem olika individer som har genomfört en mätning av något. Med fem olika resultat uppstår en osäkerhet om vad det verkliga värdet faktiskt är.
Aritmetiskt medelvärde
När du har en spridning av värden är medelvärdet ett användbart sätt att få en rimlig uppskattning av det centrala värdet.
I Excel är det enkelt att beräkna medelvärdet med funktionen MEDELVÄRDE.
Vi kan använda följande formel på vår exempeldata:
=MEDEL(B2:B6)

Standardavvikelsen för värdena
Standardavvikelsen ger oss information om hur mycket spridning det är i våra data, dvs. hur långt bort värdena typiskt befinner sig från medelvärdet.
Excel har flera funktioner för standardavvikelse, som är anpassade för olika behov. De två viktigaste är STDAV.P och STDAV.S.
Båda dessa funktioner beräknar standardavvikelsen, men skillnaden ligger i hur de tolkar data. STDAV.P förutsätter att du har hela populationen av värden, medan STDAV.S utgår ifrån att du bara har ett urval.
I vårt exempel använder vi alla fem värden, vilket innebär att vi har hela populationen och ska använda STDAV.P.
Denna funktion används på samma sätt som MEDELVÄRDE. Du kan använda formeln nedan med vår data.
=STDAV.P(B2:B6)

Resultatet, i vårt fall 0,16, visar hur mycket varje enskild mätning i genomsnitt avviker från medelvärdet.
Beräkna standardfelet
Nu när vi har standardavvikelsen kan vi beräkna standardfelet.
Standardfelet beräknas genom att dividera standardavvikelsen med kvadratroten ur antalet mätningar.
Följande formel beräknar standardfelet för våra data.
=D5/ROT(ANTAL(B2:B6))
Visualisera osäkerhet med felstaplar i diagram
Excel gör det enkelt att lägga till felstaplar i diagram för att illustrera standardavvikelser eller osäkerhetsmarginaler.
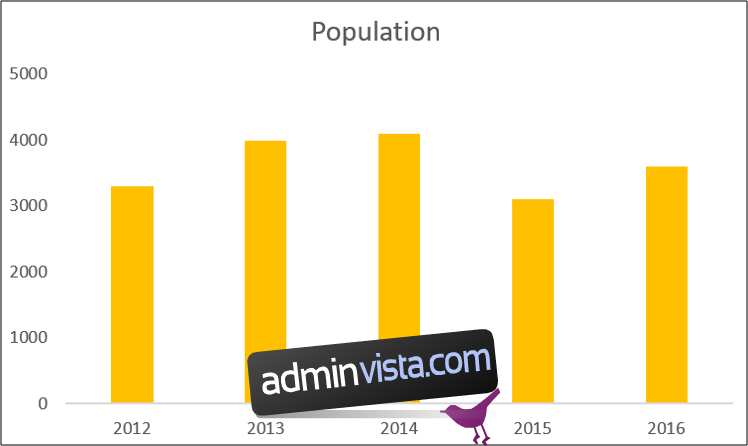
Här har vi ett stapeldiagram som visar en population som har mätts under fem år.
När diagrammet är markerat klickar du på ”Design” och sedan ”Lägg till diagramelement”.
Där kan du välja mellan olika typer av felstaplar.
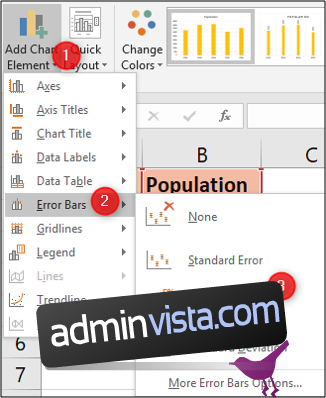
Du kan visa standardfelet eller standardavvikelsen som vi beräknade tidigare, men du kan också visa en procentuell felmarginal. Standardinställningen är 5 %.
I det här fallet valde vi att visa procenten.
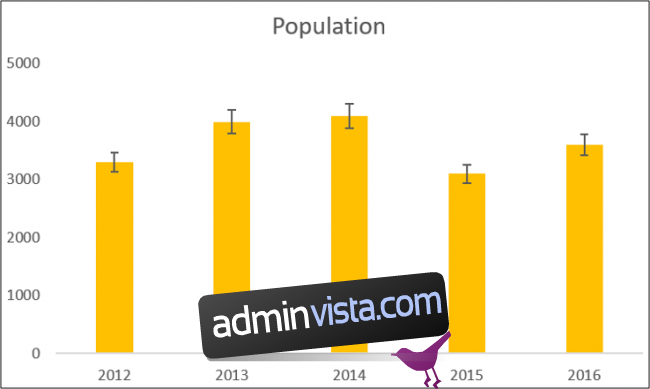
Det finns flera alternativ för att anpassa felstaplar.
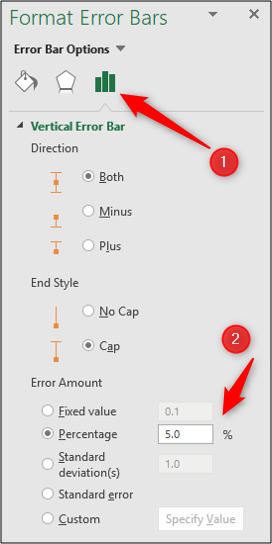
Genom att dubbelklicka på en felstapel i diagrammet öppnas menyn ”Formatera felstaplar”. Välj kategorin ”Felstapelalternativ” om den inte redan är vald.
Här kan du justera procentandelen, standardavvikelsens värde eller till och med välja ett anpassat värde från en cell som du beräknat med någon statistisk formel.
Excel är ett utmärkt verktyg för statistisk analys och rapportering. Det erbjuder en mängd metoder för att beräkna osäkerhet, så att du kan få fram den information du behöver.