Hur man skapar matriser med jämnt fördelade nummer

Denna guide kommer att visa dig hur du använder NumPy-funktionen linspace() för att generera en array med jämnt fördelade tal i Python.

Vi kommer att gå igenom syntaxen för NumPy linspace(), följt av praktiska exempel för att hjälpa dig förstå hur den fungerar.

Viktigt: För att följa den här guiden behöver du ha Python och NumPy installerade.

Saknar du NumPy? Vi har en kort installationsanvisning för dig.

Låt oss börja!

Installera och Importera NumPy

Innan vi dyker in i guiden, låt oss kort gå igenom hur du installerar NumPy-biblioteket.

⏩ Om du redan har NumPy installerat kan du gå direkt till nästa avsnitt.

• Om du använder Google Colab – en molnbaserad Jupyter Notebook-miljö – kan du importera NumPy och börja koda direkt. (Rekommenderas för denna guide ✅)
• För en lokal utvecklingsmiljö rekommenderar vi att du installerar Anaconda-distributionen av Python. Anaconda levereras med många användbara paket förinstallerade. Du kan ladda ner installationsprogrammet för ditt operativsystem. Installationen tar bara några minuter. ⌛
• Om du redan har Python installerat kan du ändå installera Anaconda-distributionen. Du kan använda conda eller pip för att installera och hantera paket. Kör ett av följande kommandon från Anacondas kommandotolk för att installera NumPy.

# Installera NumPy med conda
conda install numpy

# Installera NumPy med pip
pip install numpy

Nästa steg är att importera NumPy under aliaset np genom att köra följande kommando. Detta gör att du kan referera till NumPy som np – utan att behöva skriva ut numpy varje gång du behöver använda något från modulen.

import numpy as np

Härefter kommer vi att använda punktnotationen för att komma åt alla funktioner i NumPy-biblioteket så här: np.funktionsnamn.

Användbarheten av Jämnt Fördelade Tal

När du arbetar med NumPy-arrays kommer du ibland att behöva skapa arrays med jämnt fördelade tal inom ett visst intervall.

Innan vi går vidare, låt oss ta en snabb titt på en annan liknande funktion, np.arange().

NumPy linspace() kontra NumPy arange()

Om du har använt NumPy tidigare har du troligen använt np.arange() för att skapa en array med tal inom ett visst intervall.

Du vet att np.arange(start, stop, step) returnerar en array med tal från start till, men inte inklusive, stopp, med stegstorleken steg. Standardstegstorleken är 1.

Men stegvärdet är inte alltid lätt att veta. Låt oss se varför.

Om du till exempel behöver 4 jämnt fördelade tal mellan 0 och 1 vet du att stegstorleken måste vara 0,25. Men om du använder np.arange() så inkluderas inte stoppvärdet 1. Du måste alltså välja ett intervall som går längre än stoppvärdet.

Följande bild visar några exempel där du behöver ett specifikt antal jämnt fördelade punkter i intervallet [a, b].

Jämnt fördelade punkter inom ett intervall

Vårt första exempel med 4 jämnt fördelade punkter i [0,1] var ganska enkelt. Du vet att stegstorleken mellan punkterna ska vara 0,25.

Låt oss ta ett lite mer komplicerat exempel – där du behöver 7 jämnt fördelade punkter mellan 1 och 33. Här är kanske inte stegstorleken helt uppenbar direkt. Men du kan räkna ut stegvärdet manuellt i det här fallet.

Men np.linspace() är här för att göra det enklare för dig! 😄

Använd NumPy linspace()

När du använder np.linspace() behöver du bara ange antalet punkter du vill ha i intervallet – utan att oroa dig för stegstorleken. Och du får arrayen som du vill.

Med den förklaringen i åtanke, låt oss gå vidare och lära oss syntaxen för NumPy linspace() i nästa avsnitt.

Syntax för NumPy linspace()

Syntaxen för att använda NumPy linspace() visas nedan:

np.linspace(start, stop, num, endpoint, retstep, dtype, axis)

Till en början kan den här syntaxen se komplicerad ut med många parametrar.

De flesta av dem är dock valfria, och vi kommer att landa på en mycket enklare syntax om bara ett par minuter.

Låt oss analysera syntaxen ovan steg för steg:

• start och stop är start- respektive slutpunkten för intervallet. Både start och stop kan vara skalärer eller arrays. I denna guide kommer vi att fokusera på skalära start- och slutvärden.
• num är antalet jämnt fördelade punkter. Detta är en valfri parameter med ett standardvärde på 50.
• endpoint är också en valfri parameter som kan vara antingen True eller False.
• Standardvärdet är True, vilket betyder att slutpunkten kommer att ingå i intervallet som standard. Du kan dock sätta den till False för att utesluta slutpunkten.
• retstep är en annan valfri parameter som tar de booleska värdena True eller False. När den är satt till True returneras stegstorleken.
• dtype är datatypen för talen i arrayen. Typen antas vanligtvis vara flyttal och behöver inte anges explicit.
• axis är en annan valfri parameter som specificerar vilken axel siffrorna ska lagras längs. Detta är bara relevant när start- och stoppvärdena själva är arrays.

▶️ Så vad returnerar np.linspace()?

Den returnerar en N-dimensionell array med jämnt fördelade tal. Och om parametern retstep är inställd på True returneras även stegstorleken.

Baserat på diskussionen hittills, här är en enklare syntax för hur du kan använda np.linspace():

np.linspace(start, stop, num)

Ovanstående kodrad returnerar en array med num jämnt fördelade tal i intervallet [start, stop].

Nu när du känner till syntaxen, låt oss börja koda exempel.

Hur man Skapar Jämnt Fördelade Arrays Med NumPy linspace()

#1. Som vårt första exempel, låt oss skapa en array med 20 jämnt fördelade tal i intervallet [1, 5].

Du kan ange värdena för start, stop och num som nyckelordsargument. Detta visas i kodcellen nedan:

import numpy as np
arr1 = np.linspace(start = 1,stop = 5,num = 20)
print(arr1)

# Output:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

Observera att talen i arrayen börjar på 1 och slutar på 5 – inklusive båda slutpunkterna. Observera också att talen, inklusive 1 och 5, representeras som flyttal i den returnerade arrayen.

#2. I föregående exempel hade du angett värdena för start, stop och num som nyckelordsargument. Om du skickar argumenten i rätt ordning kan du också använda dem som positionsargument med enbart värdena, som visas nedan.

import numpy as np
arr2 = np.linspace(1,5,20)
print(arr2)

# Output:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

#3. Låt oss nu skapa en annan array där vi sätter retstep till True.

Detta betyder att funktionen nu returnerar både arrayen och stegstorleken. Och vi kan packa upp dem i två variabler arr3: arrayen, och step_size: den returnerade stegstorleken.

Följande kodcell förklarar hur du kan göra detta.

import numpy as np
arr3, step_size = np.linspace(1,5,20,retstep = True)
print(arr3)

# Output:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

# Output:
print(step_size)
0.21052631578947367

#4. Som ett sista exempel, låt oss sätta endpoint till False och se vad som händer.

import numpy as np
arr4 = np.linspace(1,5,20,endpoint = False)
print(arr4)

# Output:
[1.  1.2 1.4 1.6 1.8 2.  2.2 2.4 2.6 2.8 3.  3.2 3.4 3.6 3.8 
4.  4.2 4.4 4.6 4.8]

I den returnerade arrayen ser du att 1 ingår, men 5 ingår inte. Och det sista värdet i arrayen råkar vara 4,8, men vi har fortfarande 20 tal.

Hittills har vi bara genererat arrays med jämnt fördelade tal. I nästa avsnitt ska vi visualisera dessa siffror genom att plotta dem.

Hur man Plottar Jämnt Fördelade Tal i ett Intervall

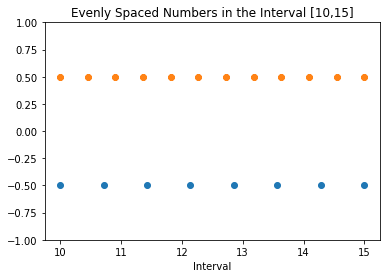
I detta avsnitt ska vi välja [10,15] som vårt intervall. Sedan använder vi np.linspace() för att generera två arrays, en med 8 respektive 12 punkter.

När det är gjort kan vi använda plottningsfunktionen från matplotlib-biblioteket för att rita dem.

För tydlighets skull kommer vi att placera de två arraysen med N1 = 8 och N2 = 12 jämnt fördelade punkter på olika positioner längs y-axeln.

Följande kodsnutt visar detta.

import numpy as np
import matplotlib.pyplot as plt

N1 = 8
N2 = 12

a = 10
b = 15

y1 = np.zeros(N1)
y2 = np.zeros(N2)

x1 = np.linspace(a, b, N1)
x2 = np.linspace(a, b, N2)

plt.plot(x1, y1-0.5, 'o')
plt.plot(x2, y2 + 0.5, 'o')

plt.ylim([-1, 1])

plt.title(f'Jämnt Fördelade Tal i Intervallet [{a},{b}]')
plt.xlabel('Intervall')

plt.show()

Att generera jämnt fördelade punkter kan vara användbart när man arbetar med matematiska funktioner. Vi kommer att lära oss mer om det i nästa avsnitt.

Hur man Använder NumPy linspace() Med Matematiska Funktioner

Efter att du har genererat en array med jämnt fördelade tal med np.linspace() kan du beräkna värdena för matematiska funktioner i intervallet.

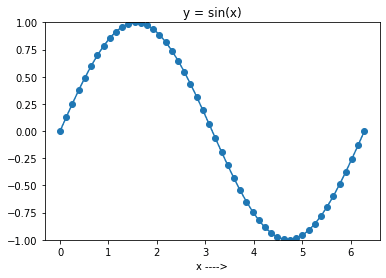
I kodcellen nedan genererar du först 50 jämnt fördelade punkter i intervallet 0 till 2π. Sedan skapar vi arrayen y med np.sin() på arrayen x. Observera att du kan hoppa över parametern num, eftersom standardvärdet är 50. Vi kommer ändå att använda den explicit här.

Som nästa steg kan du plotta sinusfunktionen i intervallet [0, 2π]. För att göra detta kan du använda matplotlib, som i föregående exempel. Specifikt används plot()-funktionen i matplotlib.pyplot för att skapa ett linjediagram.

import numpy as np
import matplotlib.pyplot as plt

N = 50

a = 0.0
b = 2*np.pi

x = np.linspace(a, b, N)
y = np.sin(x)

plt.plot(x, y, marker = "o")

plt.ylim([-1, 1])
plt.title(f'y = sin(x)')
plt.xlabel('x ---->')

plt.show()

Kör nu koden ovan genom att sätta N lika med 10. Du får diagrammet som visas i bilden nedan.

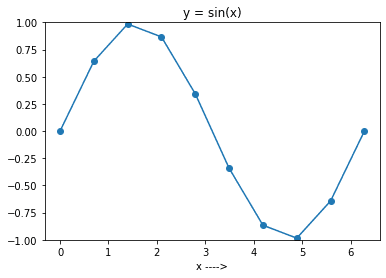
Och du kan se att plotten inte är särskilt jämn – eftersom du bara har plockat 10 punkter i intervallet.

Generellt gäller att ju fler punkter du använder, desto jämnare blir plotten av funktionen.

Sammanfattning

Här är en sammanfattning av vad vi har lärt oss:

• np.linspace(start, stop, num) returnerar en array med num jämnt fördelade tal i intervallet [start, stop].
• Sätt den valfria parametern endpoint till False för att utesluta stoppet och sätt intervallet till [start, stop).
• Sätt retstep till True för att få stegstorleken.
• Generera jämnt fördelade arrays med np.linspace() och använd sedan arrayen med matematiska funktioner.

Jag hoppas att du nu förstår hur np.linspace() fungerar. Du kan köra ovanstående exempel i en Jupyter Notebook. Kolla in vår guide om Jupyter notebook eller andra Jupyter-alternativ du kan överväga.

Vi ses snart i en annan Python-guide. Tills dess, fortsätt koda! 😀