Lär dig att multiplicera matriser i Python
I denna handledning kommer du att utforska olika metoder för att multiplicera två matriser i Python. Vi börjar med att definiera de grundläggande reglerna för matrismultiplikation och sedan skapar vi en egen Python-funktion för att hantera detta. Vi kommer också att se hur man kan uppnå samma resultat med hjälp av kapslade listkomprehensioner. Slutligen, kommer vi att dra nytta av NumPy-bibliotekets effektiva inbyggda funktioner.
Kontrollera giltigheten av matrismultiplikation
Innan vi dyker in i Python-kod, låt oss gå igenom grunderna för matrismultiplikation. Multiplikation av två matriser, A och B, är endast möjlig om antalet kolumner i matris A är lika med antalet rader i matris B.
Du har säkert stött på denna regel tidigare, men har du någonsin undrat varför den existerar? Det handlar om hur själva matrismultiplikationen utförs. Se bilden nedan.
I vårt generiska exempel har matris A ’m’ rader och ’n’ kolumner, medan matris B har ’n’ rader och ’p’ kolumner.
Formen på den resulterande matrisen
Elementet vid index (i, j) i den resulterande matrisen C beräknas genom punktprodukten av rad ’i’ i matris A och kolumn ’j’ i matris B. För att beräkna ett element vid ett givet index i C, måste vi alltså ta punktprodukten av den motsvarande raden och kolumnen i A respektive B. Denna process upprepas för alla element för att skapa C, som har dimensionerna m x p (m rader och p kolumner), som illustreras nedan.
Punktprodukten (eller den inre produkten) av två vektorer a och b ges av följande formel:

Låt oss sammanfatta:
- Punktprodukten kan endast beräknas mellan vektorer av samma längd.
- För att punktprodukten mellan en rad och en kolumn ska vara giltig vid matrismultiplikation måste båda ha lika många element.
- I vårt exempel har varje rad i matris A ’n’ element, och varje kolumn i matris B har också ’n’ element.
Det är därför antalet kolumner i matris A måste vara lika med antalet rader i matris B.
Jag hoppas att du nu förstår varför denna regel existerar och hur varje element i den resulterande matrisen skapas. Låt oss nu gå vidare och implementera detta i Python.
Skapa en anpassad Python-funktion för matrismultiplikation
Vi börjar med att skriva en egen funktion för att multiplicera matriser. Funktionen bör:
- Ta två matriser, A och B, som indata.
- Verifiera om matrismultiplikationen mellan A och B är giltig.
- Om giltig, beräkna produkten av A och B, och returnera matrisen C.
- Annars, returnera ett felmeddelande.
Steg 1: Generera två matriser med hjälp av NumPy’s random.randint() eller definiera dem som kapslade Python-listor.
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f"Matrix A:\n {A}\n")
print(f"Matrix B:\n {B}\n")
# Output
# Matrix A:
# [[4 9 9]
# [9 1 6]
# [9 2 3]]
#
# Matrix B:
# [[2 2]
# [5 7]
# [4 4]]
Steg 2: Definiera funktionen multiply_matrix(A,B) som returnerar produktmatrisen C om multiplikationen är giltig.
def multiply_matrix(A,B):
global C
if A.shape[1] == B.shape[0]:
C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
for row in range(A.shape[0]):
for col in range(B.shape[1]):
for elt in range(B.shape[0]):
C[row, col] += A[row, elt] * B[elt, col]
return C
else:
return "Matriserna kan inte multipliceras."
Analys av funktionsdefinitionen
Låt oss undersöka funktionsdefinitionen i detalj.
Global variabeldeklaration: I Python har variabler i funktioner lokalt omfång. För att göra matrisen C tillgänglig utanför funktionen måste vi deklarera den som en global variabel med nyckelordet ’global’.
Kontroll av multiplikationsgiltighet: Använd attributet ’shape’ för att kontrollera om A och B kan multipliceras. ’arr.shape[0]’ och ’arr.shape[1]’ anger antalet rader respektive kolumner. Om ’A.shape[1] == B.shape[0]’ är sant, fortsätter vi med beräkningen, annars returneras ett felmeddelande.
Kapslade loopar: För att beräkna elementen i matrisen C går vi igenom rader i A (yttre loop), kolumner i B (inre loop), och element i en vald kolumn i B (innersta loop).
Nu när vi har förstått funktionen, låt oss anropa den med de matriser vi genererade tidigare.
multiply_matrix(A,B) # Output # array([[ 89, 107], # [ 47, 49], # [ 40, 44]])
Eftersom multiplikationen är giltig, returnerar funktionen resultatet.
Multiplicera matriser med kapslade listkomprehensioner
Förutom funktionen kan vi också multiplicera matriser med kapslade listkomprehensioner.
Här är koden:
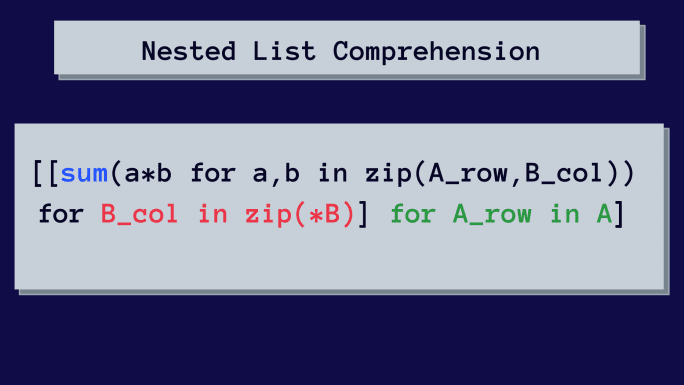
Detta kan verka komplicerat, men vi ska analysera det steg för steg. Vi använder denna mall för att analysera listan:
[<gör-detta> for <element> in <iterable>] där, <gör-detta>: uttryck eller operation <element>: varje element du vill utföra operationen på <iterable>: listan, tupeln, eller liknande som du itererar genom
Se vår guide om listkomprehensioner i Python för en djupare förståelse.
Vi vill bygga matrisen C rad för rad.
Kapslade listkomprehensioner förklaras
Steg 1: Beräkna ett enskilt värde i matrisen C
För rad ’i’ i A och kolumn ’j’ i B, ger uttrycket nedan elementet vid (i,j) i C.
sum(a*b for a,b in zip(A_row, B_col)) # zip(A_row, B_col) returnerar en iterator av tupler. # Om A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returnerar (a1, b1), (a2, b2) etc
Om i=j=1 returnerar uttrycket c_11 i matris C. Du kan få ett enskilt element per rad.
Steg 2: Skapa en rad i matrisen C
För rad 1 i A måste du iterera genom alla kolumner i B för att få en komplett rad i C.
Använd listkomprehensionsmallen:
- Ersätt
med uttrycket från steg 1. - Ersätt
med B_col—varje kolumn i matris B. - Ersätt
med zip(*B)—listan som innehåller alla kolumner i B.
Och här är den första listkomprehensionen:
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * är unzipping operatorn # zip(*B) returnerar en lista av kolumner i B
Steg 3: Bygg hela matrisen C
För att fylla ut C måste du beräkna resten av raderna och iterera genom A:s rader.
Använd listkomprehension igen:
- Ersätt
med listkomprehension från steg 2. - Ersätt
med A_row—varje rad i A. är matrisen A när du itererar genom dess rader.
Och här är den fullständiga kapslade listkomprehensionen:
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]
Nu verifierar vi resultatet: ✔
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# Output:
#[[ 89 107]
# [ 47 49]
# [ 40 44]]
Detta motsvarar de kapslade looparna, fast mer koncist. I nästa avsnitt ska vi se mer effektiva inbyggda funktioner.
Använd NumPy’s matmul() för matrismultiplikation
Funktionen np.matmul() tar två matriser som indata och returnerar produkten om multiplikationen är giltig.
C = np.matmul(A,B) print(C) # Output: #[[ 89 107] # [ 47 49] # [ 40 44]]
Denna metod är enklare än de tidigare. Vi kan även använda en motsvarande @-operator.
Använda @-operatorn för matrismultiplikation
I Python är @ en binär operator för matrismultiplikation. Den fungerar med två matriser (N-dimensionella NumPy-matriser) och returnerar produktmatrisen. Du behöver Python 3.5 eller senare för att använda @-operatorn.
Användning:
C = A @ B print(C) # Output # array([[ 89, 107], # [ 47, 49], # [ 40, 44]])
Som du ser får vi samma resultat.
Kan man använda np.dot() för att multiplicera matriser?
Du kanske har sett kod som använder np.dot() för att multiplicera matriser. Så här fungerar det:
C = np.dot(A,B) print(C) # Output: #[[ 89 107] # [ 47 49] # [ 40 44]]
Även om np.dot(A,B) ger det förväntade resultatet, bör den enligt NumPy-dokumentationen enbart användas för punktprodukter av endimensionella vektorer. Eftersom NumPy implicit överför denna operation till alla rader och kolumner får du rätt produktmatris, men för att hålla koden läsbar och tydlig bör du använda np.matmul() eller @-operatorn istället.
Sammanfattning
🎯 I den här handledningen har du lärt dig:
- Villkoret för giltig matrismultiplikation: antal kolumner i A = antal rader i B.
- Skapa en Python-funktion som kontrollerar om multiplikation är giltig och returnerar produktmatrisen (med kapslade for-loopar).
- Använda kapslade listkomprehensioner för att multiplicera matriser, vilket är mer koncist men kan vara mindre läsbart.
- Använda NumPy’s np.matmul() för effektiv matrismultiplikation.
- Använda @-operatorn i Python för matrismultiplikation.
Detta avslutar vår diskussion om matrismultiplikation i Python. Nu kan du fortsätta med att lära dig mer, till exempel hur du kontrollerar om ett tal är ett primtal i Python eller utforska intressanta problem med strängar.
Lycka till med lärandet!🎉