Hypotesprövning är ett verktyg som används flitigt av analytiker inom både den privata och offentliga sektorn för att dra slutsatser och göra antaganden om populationsdata.
Om du har arbetat med eller studerat populationsdata, har du säkert stött på detta viktiga verktyg.
Det finns många metoder för att dra slutsatser, men inte alla garanterar hög precision.
Om du är osäker på din data, men ändå vill använda den, kan det vara riskabelt för din organisation.
Hypotesprövning är en utmärkt strategi för att uppnå en högre grad av noggrannhet och har varit avgörande för befolkningsanalys.
I den här artikeln kommer jag att gå igenom vad hypotesprövning är, hur den fungerar, dess fördelar och olika användningsområden.
Så, låt oss sätta igång!
Vad är hypotesprövning?
Hypotesprövning är en statistisk metod som analytiker använder för att avgöra om tillgänglig populationsdata ger tillräckligt stöd för en specifik hypotes och för att dra slutsatser.
Med denna metod kan analytiker enkelt bedöma en hypotes och avgöra hur pass korrekt antagandet är, baserat på den tillgängliga datan.
Enkelt uttryckt är det en testprocess som bygger på inferentiell statistik och som gör det möjligt att dra en slutsats om populationsdata baserat på insamlad provdata.
Det är i praktiken nästan omöjligt för analytiker att undersöka egenskaper eller en specifik parameter för en hel population. Men genom hypotesprövning kan du göra välgrundade förutsägelser och fatta beslut baserat på provdata och dess noggrannhet.
Olika typer av hypotesprövning
Här är de olika typerna av hypotesprövning:
- Nollhypotes: Denna statistik indikerar att det inte finns något samband mellan de två variablerna i den givna provdatan och att den observerade datan är slumpmässig.
- Alternativ hypotes: Denna hypotes presenterar den primära tesen och motsäger nollhypotesen. Den är drivkraften i testprocessen och visar en korrelation mellan två variabler i provdata.
- Icke-riktningshypotes: Denna typ av hypotesprövning fungerar som en tvåsidig hypotes. Den visar att det inte finns någon specificerad riktning mellan två variabler i provdata och att det sanna värdet skiljer sig från det förutsagda värdet.
- Riktningshypotes: En riktningshypotes visar ett specifikt samband mellan två variabler. Här kan en variabel i ett urvalsdata påverka andra variabler.
- Statistisk hypotes: Denna hypotes hjälper analytiker att utvärdera om data och värde uppfyller en viss hypotes. Den är mycket användbar för att göra uttalanden och antaganden om resultatet av en stickprovspopulationsparameter.
Låt oss nu utforska de olika metoderna för hypotesprövning.
Metoder för hypotesprövning
För att bedöma om en viss hypotes är sann eller inte, behöver analytiker en betydande mängd trovärdig bevisning innan de kan dra en slutsats. I denna testprocess formuleras en nollhypotes och en alternativ hypotes innan själva bedömningen startar.
Hypotesprövning omfattar en mängd olika metoder för att bedöma om urvalsdata är gynnsamma. Analytiker måste ta hänsyn till både data och urvalsstorlek och välja den hypotesprövningsmetod som passar bäst för situationen.
Normalitetstestning
Detta är en standardmetod för hypotesprövning som används för att analysera den regelbundna fördelningen i provdata. Under testprocessen undersöks om de grupperade datapunkterna runt medelvärdet är över eller under medelvärdet.
I denna statistiska testning är sannolikheten att en datapunkt hamnar över eller under medelvärdet lika stor. En klockkurva bildas, och den är jämnt fördelad på båda sidor om medelvärdet.
Z-test
Detta är en annan typ av hypotesprövning som används när populationsdata är normalfördelad. Den testar om medelvärdet för två separata populationsparametrar skiljer sig åt, när variansen av data är känd.
När man analyserar populationsdata är det vanligt att använda detta test när urvalsstorleken är större än trettio. Den centrala gränssatsen är en annan anledning till att Z-testet är lämpligt, eftersom den satsen säger att när urvalsstorlekarna ökar blir stickproven normalfördelade.
T-test
T-test hypotesprövning används när urvalsstorleken är begränsad och vanligtvis distribuerad. Oftast används denna metod när urvalsstorleken är under 30 och standardavvikelsen för parametern är okänd.
T-test används för att beräkna konfidensintervall för specifika populationsdata.
Chi-kvadrattest
Chi-kvadrattestet är en populär metod för hypotesprövning som ofta används för att bedöma lämpligheten och integriteten i en distribution av data.
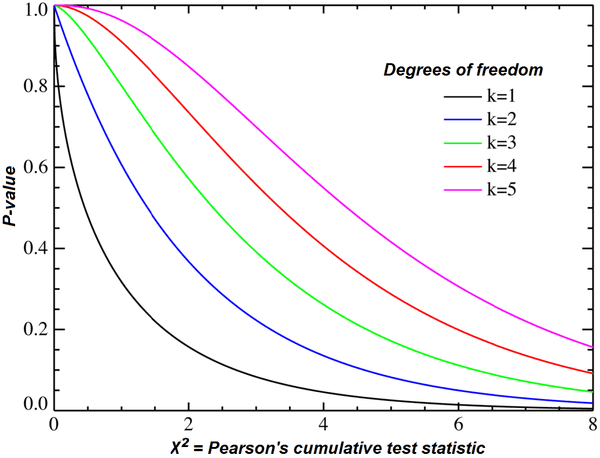
Källa: wikipedia.org
Den främsta anledningen att använda denna typ av hypotesprövning är när man vill testa populationsvariansen mot en känd eller antagen populationsvarians. Det finns olika typer av Chi-kvadrattest, men de vanligaste är Chi-kvadrat testet för varians och oberoende.
ANOVA-testning

Förkortat som Analys av varians, är detta en statistisk metod som hjälper till att jämföra datamängder för två eller fler prover. Det ger möjlighet att jämföra fler än två variabler samtidigt.
Det förklarar även en beroende variabel och en oberoende variabel för provdata. Användningen av ANOVA är ganska lik användningen av Z-test och T-test, men de två sistnämnda är begränsade till endast två variabler.
Hur fungerar hypotesprövning?
Analytiker som använder hypotesprövning använder slumpmässigt urval för analys och mätning. Under testningen används slumpmässiga urvalsdata för att testa nollhypotesen och den alternativa hypotesen.
Som vi tidigare har nämnt är nollhypotesen och den alternativa hypotesen helt uteslutande, och under testresultatet kan endast en vara sann.
Det finns dock vissa fall då nollhypotesen förkastas, men den alternativa hypotesen inte alltid är sann.
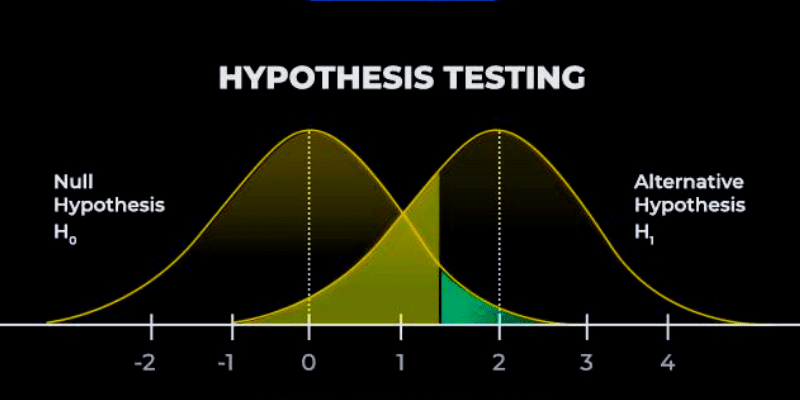
Källa: Analytics Steps
P-värde: När testprocessen inleds, används p-värdet, eller sannolikhetsvärdet. Det indikerar om resultatet är signifikant eller inte. P-värdet visar även sannolikheten för att fel uppstår när en nollhypotes förkastas eller inte förkastas under testningen. Det resulterande p-värdet är antingen 0 eller 1, och det jämförs sedan med signifikansnivån, eller alfanivån.
Signifikansnivån definierar den acceptabla risken vid förkastandet av en nollhypotes under testningen. Det är viktigt att komma ihåg att resultatet av hypotesprövningen kan leda till två typer av fel:
- Typ 1-fel uppstår när testresultatet förkastar nollhypotesen, trots att den är sann.
- Typ 2-fel uppstår när nollhypotesen accepteras av provresultatet, trots att den är falsk.
Alla värden som leder till att nollhypotesen förkastas, lagras i det kritiska området, och det kritiska värdet skiljer de kritiska områdena från andra.
Steg för att utföra hypotesprövning
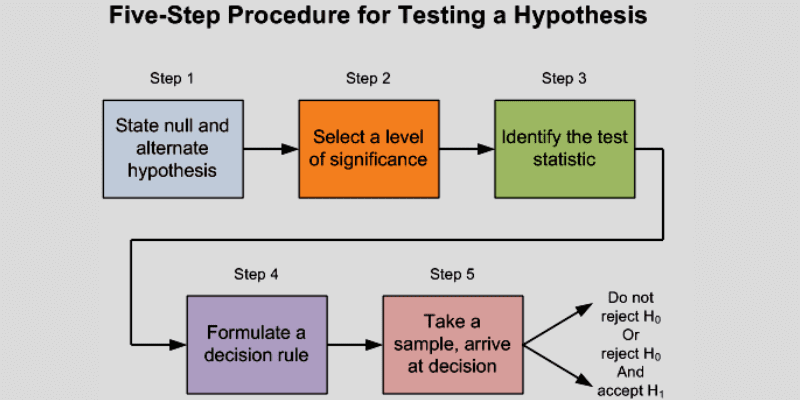
Källa: Medium
Hypotesprövning omfattar huvudsakligen fyra steg:
- Definiera hypoteser: I det första steget måste analytikern definiera de två hypoteserna, så att bara en kan vara sann. Nollhypotesen anger att det inte finns någon skillnad i medel-BMI, medan den alternativa hypotesen kommer att ange att det finns en signifikant skillnad i medel-BMI.
- Plan: I nästa steg måste man utforma en analysplan för hur provdatan ska analyseras. Det är viktigt att man gör ett urval och samlar in provdata som lämpar sig för att testa hypotesen.
- Analysera provdata: Efter att ha bestämt hur man ska utvärdera data, är det dags att börja själva processen. Analysera provdatan noggrant så att det inte finns någon överflödig information. Se till att urvalen är oberoende av varandra och att båda urvalsstorlekarna är tillräckligt stora.
- Beräkna teststatistik: I detta skede beräknas teststatistiken och p-värdet. P-värdet bestäms genom att anta att nollhypotesen är sann.
- Bedöm resultatet: I det sista steget ska testresultatet bedömas och man avgör om nollhypotesen ska förkastas eller om den är rimlig, baserat på provdatan.
Låt oss nu utforska fördelarna med hypotesprövning.
Fördelar med hypotesprövning
Här är fördelarna med hypotesprövning:
- Det hjälper till att analysera styrkan i ett påstående baserat på data.
- Analytiker kan skapa en pålitlig miljö för att fatta beslut baserat på provdata.
- Metoden ger möjlighet att avgöra om den provdata som ingår i hypotesprövningen är statistiskt signifikant.
- Den är fördelaktig för att bedöma tillförlitligheten och giltigheten hos testresultat i alla systematiska testprocesser.
Metoden hjälper till att extrapolera data från ett urval till en större population, beroende på behovet.
Användningsområden för hypotesprövning
Hypotesprövning används inom en rad olika sektorer för att bedöma korrektheten hos provdata. Här är några verkliga exempel på hypotesprövning:
#1. Kliniska tester
Hypotesprövning används ofta i kliniska tester, eftersom det hjälper vårdpersonal att avgöra om ett nytt läkemedel, en ny behandling eller ett nytt förfarande kommer att vara effektivt, baserat på provdata.
En läkare kan tro att en behandling kan sänka kaliumnivåerna hos vissa patienter. Läkaren mäter då kaliumnivån hos en grupp patienter innan behandlingen inleds och kontrollerar nivån igen efteråt.

Därefter utför läkaren en hypotesprövning där H0: Uefter = Uföre, vilket innebär att kaliumnivån är densamma som tidigare efter appliceringen av behandlingen. En annan hypotes indikerar att Ha: Uefter < Uföre, vilket betyder att kaliumnivån har sjunkit efter behandlingen.
Om p-värdet är lägre än signifikansnivån kan läkaren dra slutsatsen att behandlingen kan sänka kaliumnivån.
#2. Tillverkning
Hypotesprövning används inom tillverkningsanläggningar för att hjälpa handledare att avgöra om en ny metod eller teknik är effektiv eller inte.
Till exempel kan vissa tillverkningsenheter använda hypotesprövning för att ta reda på om en ny metod hjälper dem att minska antalet defekta produkter per batch. Låt oss anta att antalet defekta produkter är 300 per batch.

Tillverkaren måste bestämma medelvärdet för det totala antalet defekta produkter som producerats före och efter att ha infört en ny metod. De utför en hypotesprövning och använder hypoteserna H0: Uefter = Uföre, där medelvärdet för defekta produkter som produceras efter en ny metod är samma som tidigare.
En annan hypotes visar att HA: Uefter inte är lika med Uföre, vilket betyder att det totala antalet defekta produkter som produceras efter en ny metod har förändrats.
Efter testet, om p-värdet är lägre än signifikansnivån, kan tillverkningsenheten dra slutsatsen att antalet defekta produkter som produceras har förändrats.
#3. Jordbruk
Hypotesprövning används ofta för att ta reda på om gödningsmedel eller bekämpningsmedel påverkar växters tillväxt och immunitet. Biologer kan använda testet för att bevisa att en viss växt kan växa mer än 15 tum efter att ha fått ett nytt gödningsmedel.

Biologen kan applicera gödselmedlet under en månad för att samla in provdata. När en hypotesprövning utförs kan en hypotes vara H0 U = 15 tum, vilket indikerar att gödselmedlet inte ger någon förbättring av växtens medeltillväxt.
En annan hypotes visar att HA: U > 15 tum, vilket betyder att gödselmedlet förstärker växtens medeltillväxt. Efter testet, när p-värdet är lägre än signifikansnivån, kan biologen bevisa att gödselmedlet orsakar mer tillväxt än tidigare.
Lärresurser
#1. Statistik: En steg-för-steg-introduktion av Udemy

Udemy erbjuder en kurs i statistik som ger en steg-för-steg introduktion till ämnet, som även täcker hypotesprövning. Kursen har exempel och lärdomar från en före detta dataforskare på Google, som hjälper dig att bemästra konfidensintervall, hypotesprövning med mera.
#2. Viktig statistik för dataanalys av Udemy
Den här kursen på Udemy om viktig statistik för dataanalys hjälper dig att lära dig statistik med hjälp av verkliga projekt, roliga aktiviteter, hypotesprövning, sannolikhetsfördelningar, regressionsanalys med mera.
#3. Statistik för datavetenskap och affärsanalys

Denna kurs om statistik för datavetenskap och affärsanalys erbjuds av Udemy och hjälper dig att lära dig hypotesprövning. Den täcker olika statistiska ämnen, vilket gör det möjligt för datavetare och affärsanalytiker att lära sig och bemästra dem. Den täcker inferentiell och beskrivande statistik, samt regressionsanalys.
#4. Hypothesis Testing av Jim Frost
Denna bok finns tillgänglig på Amazon och är en intuitiv guide som hjälper analytiker att fatta datadrivna beslut.
Den förklarar hur hypotesprövning fungerar, varför den behövs och hur man effektivt använder konfidensintervall, p-värden, signifikansnivåer och många fler ämnen.
#5. Hypothesis Testing av Scott Hartshorn
Denna bok är unik med sina visuella exempel och är bäst för nybörjare som söker en snabbguide om hypotesprövning.
Den introducerar betydelsen av statistik, dess typer och hur den fungerar. Det krävs inte några förkunskaper inom statistik, och allt förklaras på ett intuitivt sätt.
Avslutande ord
Hypotesprövning hjälper till att verifiera ett antagande och utveckla statistisk data baserat på bedömningen. Metoden används i många sektorer, från tillverkning och jordbruk till kliniska tester och IT. Denna metod är inte bara exakt, utan den hjälper dig också att fatta datadrivna beslut för din organisation.
Kolla in de olika inlärningsresurserna för att bli en affärsanalytiker.