Hur man kontrollerar om ett tal är primtal i Python

Innehållsförteckning

Den här guiden kommer att lära dig hur man skapar ett Pythonprogram som avgör om ett givet tal är ett primtal eller inte.

Om du någon gång har stött på programmeringstester, har du säkert sett matematikfrågor som handlar om att undersöka om ett tal är ett primtal. Under de kommande minuterna kommer du att lära dig att utveckla den mest effektiva lösningen på detta problem.

I den här handledningen kommer du att:

Granska grunderna i primtal.
Skriva Python-kod för att fastställa om ett tal är ett primtal.
Optimera koden för att uppnå en algoritm med körtidskomplexitet O(√n).

Med det sagt, låt oss börja!

Vad är ett primtal?

Låt oss börja med att gå igenom de grundläggande definitionerna av primtal.

Inom talteorin definieras ett naturligt tal n som primtal om det har exakt två faktorer: 1 och talet självt (n). Kom ihåg från din matematikundervisning att ett tal i sägs vara en faktor av talet n om i delar n jämnt. ✅

I tabellen nedan visas några tal, deras faktorer och om de är primtal eller inte.

n	Faktorer	Är det primtal?
1	1	Nej
2	1, 2	Ja
3	1, 3	Ja
4	1, 2, 4	Nej
7	1, 7	Ja
15	1, 3, 5, 15	Nej

Från tabellen ovan kan vi dra följande slutsatser:

2 är det minsta primtalet.
1 är en faktor i varje tal.
Varje tal n är en faktor av sig självt.

Alltså är 1 och n triviala faktorer för varje tal n. Ett primtal ska inte ha några andra faktorer än dessa två.

Detta betyder att när man undersöker tal från 2 till n-1, ska man inte hitta någon icke-trivial faktor som delar n utan rest.

O(n) Algoritm för att kontrollera om ett tal är primtal i Python

I det här avsnittet kommer vi att formalisera det ovanstående tillvägagångssättet i en Python-funktion.

Du kan undersöka alla tal från 2 till n-1 med hjälp av range()-funktionen i Python.

I Python returnerar range(start, stop, step) ett range-objekt. Du kan sedan iterera över detta objekt för att få en sekvens av tal från start upp till stop-1, i steg som anges i step.

Eftersom vi behöver en sekvens av heltal från 2 till n-1, kan vi ange range(2, n) och använda det tillsammans med en for-loop.

Här är vad vi vill göra:

Om du hittar ett tal som delar n jämnt utan rest, kan du direkt slå fast att talet inte är ett primtal.

Om du har gått igenom hela intervallet av tal från 2 upp till n-1 utan att hitta något tal som delar n jämnt, då är talet ett primtal.

Python-funktion för att kontrollera primtal

Med ovanstående som grund kan vi nu definiera funktionen is_prime() som följer:

def is_prime(n):
  for i in range(2,n):
    if (n%i) == 0:
      return False
  return True

Låt oss analysera funktionsdefinitionen ovan:

Funktionen is_prime() tar ett positivt heltal n som argument.
Om en faktor hittas inom det angivna intervallet (2, n-1) returnerar funktionen False eftersom talet inte är ett primtal.
Funktionen returnerar True om loopen går igenom hela intervallet utan att hitta en faktor.

Låt oss sedan anropa funktionen med olika argument och kontrollera att utdata är korrekt.

is_prime(2)
# True

is_prime(8)
# False

is_prime(9)
# False

is_prime(11)
# True

I utdata ovan ser du att 2 och 11 är primtal (funktionen returnerar True), medan 8 och 9 inte är primtal (funktionen returnerar False).

Hur man optimerar Python-funktionen is_prime()

Vi kan göra en liten optimering här. Notera listan över faktorer i tabellen nedan:

Tal	Faktorer
6	1, 2, 3, 6
10	1, 2, 5, 10
18	1, 2, 3, 6, 9, 18

Vi kan se att den enda faktorn för n som är större än n/2 är n själv.

Det betyder att du inte behöver loopa hela vägen upp till n-1. Du kan istället bara loopa upp till n/2.

Om du inte hittar en icke-trivial faktor förrän n/2, kommer du inte att hitta någon bortom n/2 heller.

Låt oss nu ändra funktionen is_prime() för att leta efter faktorer i intervallet (2, n/2):

def is_prime(n):
  for i in range(2,int(n/2)):
    if (n%i) == 0:
      return False
  return True

Låt oss fortsätta och verifiera resultatet med några funktionsanrop:

is_prime(9)
# False

is_prime(11)
# True

Även om det kan verka som att vi har optimerat, är den här algoritmen inte mer effektiv än den tidigare när det gäller tidskomplexitet. Båda har faktiskt en tidskomplexitet på O(n), vilket är proportionellt mot värdet på n.

Kan vi göra det bättre? Ja, det kan vi!

▶️ Fortsätt till nästa avsnitt för att lära dig hur man förbättrar tidskomplexiteten för primtalstester.

O(√n) Algoritm för att kontrollera primtal i Python

Faktorerna för ett tal förekommer ofta i par.

Om a är en faktor i talet n, finns det också en faktor b så att a * b = n, eller helt enkelt ab = n.

Låt oss verifiera detta med ett exempel.

Tabellen nedan visar faktorerna för talet 18, där de förekommer i par. Du kan verifiera detta med fler tal om du vill.

Notera också att √18 är ungefär 4.24.

I faktorparen (a, b) kan du se att om a är mindre än 4.24 så är b större än 4.24 – till exempel (2, 9) och (3, 6) i det här fallet.

Faktorer för 18 i par:

Figuren nedan visar faktorerna för 18 på en tallinje.

Om talet n råkar vara en perfekt kvadrat, har du a = b = √n som en av faktorerna.

▶️ Titta på faktorerna för 36 i tabellen nedan. Eftersom 36 är en perfekt kvadrat, är a=b=6 en av faktorerna. För alla andra faktorpar (a,b) gäller a < 6 och b > 6.

Faktorer för 36 i par:

Sammanfattningsvis gäller följande:

Varje tal n kan skrivas som n = a * b
Om n är en perfekt kvadrat är a = b = √n.
Om a < b, då är a < √n och b > √n.
Om a > b, då är a > √n och b < √n.

Så istället för att iterera över alla heltal upp till n/2, kan du istället välja att iterera upp till √n. Detta är mycket effektivare än vårt tidigare tillvägagångssätt.

Hur man ändrar algoritmen is_prime() till O(√n)

Låt oss nu optimera funktionen för att hitta primtal i Python.

import math
def is_prime(n):
  for i in range(2,int(math.sqrt(n))+1):
    if (n%i) == 0:
      return False
  return True

Låt oss analysera funktionsdefinitionen ovan:

För att beräkna kvadratroten av ett tal, importerar vi Pythons inbyggda matematikmodul och använder funktionen math.sqrt().
Eftersom n kanske inte är en perfekt kvadrat, måste vi konvertera resultatet till ett heltal. Använd int(var) för att konvertera var till en int.
För att vara säkra på att vi faktiskt undersöker upp till √n, lägger vi till plus ett eftersom range() som standard exkluderar intervallets slutpunkt.

Kodavsnittet nedan verifierar att vår funktion is_prime() fungerar korrekt.

is_prime(8)
# False

is_prime(15)
# False

is_prime(23)
# True

I nästa avsnitt skapar vi några enkla diagram för att visualisera O(n) och O(√n).

Jämföra O(n) och O(√n) visuellt

▶️ Kör följande kod i en Jupyter Notebook eller liknande miljö:

import numpy as np
import seaborn as sns
import pandas as pd


n = 20

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

Ovanstående utdrag visar hur man kan rita kurvorna för n och √n för ett visst intervall.

Vi använder NumPy-funktionen arange() för att skapa en array med tal.
Sedan samlar vi värdena för n och √n upp till, men inte inklusive, 20, i en Pandas DataFrame.
Slutligen ritar vi med hjälp av Seaborns lineplot()-funktion.

Från diagrammet nedan ser vi att √n är betydligt mindre än n.

Låt oss nu öka intervallet till 2000 och upprepa samma steg som ovan:

import numpy as np
import seaborn as sns
import pandas as pd


n = 2000

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

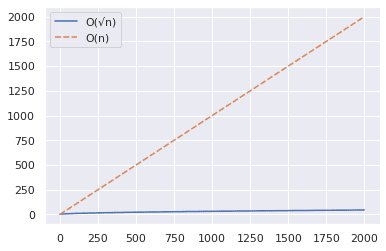
Från diagrammet ovan kan vi se att O(√n)-algoritmen är betydligt snabbare när det gäller att undersöka om ett stort tal är ett primtal.

Här är ett snabbt exempel: 2377 är ett primtal. Verifiera det! 😀

Medan O(n)-metoden tar ungefär 2000 steg, kan O(√n)-algoritmen hitta svaret på bara 49 steg.✅

Slutsats

⏳ Då är det dags för en snabb sammanfattning.

För att kontrollera om ett tal är ett primtal, är den enklaste metoden att iterera över alla tal i intervallet (2, n-1). Om du inte hittar en faktor som delar n, är n ett primtal.
Eftersom den enda faktorn av n som är större än n/2 är n självt, kan du välja att endast loopa upp till n/2.
Båda tillvägagångssätten har en tidskomplexitet på O(n).
Eftersom faktorerna i ett tal förekommer i par, kan du välja att endast loopa upp till √n. Denna algoritm är mycket snabbare än O(n). Skillnaden blir tydlig när man undersöker om ett stort tal är ett primtal eller inte.

Jag hoppas att du nu förstår hur man kontrollerar om ett tal är ett primtal i Python. Som nästa steg kan du kolla in vår handledning om Python-program för strängoperationer – där du får lära dig att kontrollera om strängar är palindromer, anagram och mer.

Vi ses i en annan handledning. Tills dess, lycka till med kodningen! 👩🏽‍💻