Excel erbjuder inbyggda verktyg som underlättar visualisering av kalibreringsdata och beräkning av en optimal anpassningslinje. Detta är särskilt användbart vid sammanställning av kemiska labbrapporter eller vid programmering av korrigeringsfaktorer i utrustning.
Denna artikel beskriver hur du nyttjar Excel för att skapa diagram, konstruera en linjär kalibreringskurva, presentera formeln för kalibreringskurvan och implementera enkla formler med hjälp av funktionerna SLUTTNING och SKÄRNING för att tillämpa kalibreringsekvationen i Excel.
Vad är en kalibreringskurva och hur bidrar Excel vid skapandet?
En kalibrering innebär att man jämför avläsningar från en enhet (t.ex. en termometers temperaturvisning) med kända referensvärden, kallade standarder (som vattnets fryspunkt och kokpunkt). Detta resulterar i en samling datapunkter som sedan används för att generera en kalibreringskurva.
En tvåpunktskalibrering av en termometer, med utgångspunkt i vattnets frys- och kokpunkt, skulle generera två datapunkter: en vid termometerns placering i isvatten (0°C) och en i kokande vatten (100°C). Genom att plotta dessa datapunkter och dra en linje mellan dem (kalibreringskurvan), under förutsättning att termometerns respons är linjär, kan man tolka vilken punkt som helst på linjen som korresponderar till termometerns avläsning, och därmed få fram den motsvarande ”korrekta” temperaturen.
Linjen i sig interpolerar värden mellan de två kända punkterna, vilket möjliggör tillförlitliga uppskattningar av den faktiska temperaturen, även när termometern visar ett värde som inte motsvarar en direkt uppmätt ”standard” (t.ex. 57,2 grader).
Excel har kapacitet att visuellt plotta datapunkter i ett diagram, lägga till en trendlinje (kalibreringskurvan) och visa kalibreringskurvans ekvation direkt i diagrammet. Förutom den visuella aspekten kan linjens formel beräknas med Excels funktioner SLUTTNING och SKÄRNING. Genom att implementera dessa värden i enkla formler, kan ”korrekta” värden automatiskt beräknas utifrån alla mätningar.
Ett praktiskt exempel
I det här exemplet kommer vi att skapa en kalibreringskurva baserad på tio datapunkter, där varje punkt består av ett X-värde och ett Y-värde. X-värdena fungerar som våra ”standarder” och kan representera allt från koncentrationen av en kemisk lösning uppmätt med ett vetenskapligt instrument, till ett inmatningsvärde för ett program som kontrollerar en maskin som skjuter ut kulor.
Y-värdena utgör ”svaren” och kan representera instrumentets avläsning vid mätning av varje kemisk lösning, eller det uppmätta avståndet kulan landade från utskjutningsrampen vid olika inmatningsvärden.
Efter att kalibreringskurvan visualiserats, kommer vi att använda SLUTTNING- och SKÄRNING-funktionerna för att bestämma kalibreringslinjens formel och fastställa koncentrationen av en ”okänd” kemisk lösning baserat på instrumentets avläsning, eller välja ett lämpligt inmatningsvärde för programmet så att kulan landar på ett specificerat avstånd från utskjutaren.
Steg ett: Skapa diagrammet
Vår enkla kalkylblad består av två kolumner, ”X-Värde” och ”Y-Värde”.
Låt oss börja med att välja den data som ska representeras i diagrammet.
Markera först cellerna i kolumnen ”X-Värde”.
Håll nu ned Ctrl-tangenten och klicka på cellerna i kolumnen ”Y-Värde”.
Gå till fliken ”Infoga”.
Navigera till ”Diagram”-menyn och välj det första alternativet i rullgardinsmenyn ”Punkt”.
Ett diagram med datapunkterna från de två kolumnerna visas.
Markera serien genom att klicka på en av de blå punkterna. De markerade punkterna kommer att ramas in.
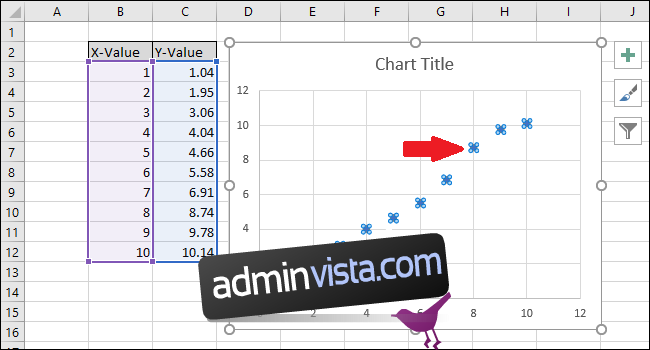
Högerklicka på en av punkterna och välj ”Lägg till trendlinje”.
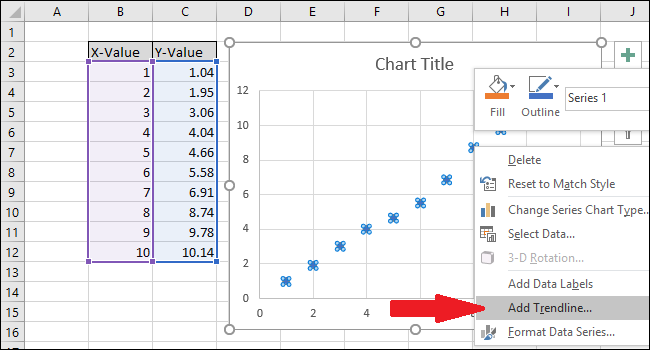
En rät linje kommer nu att synas i diagrammet.
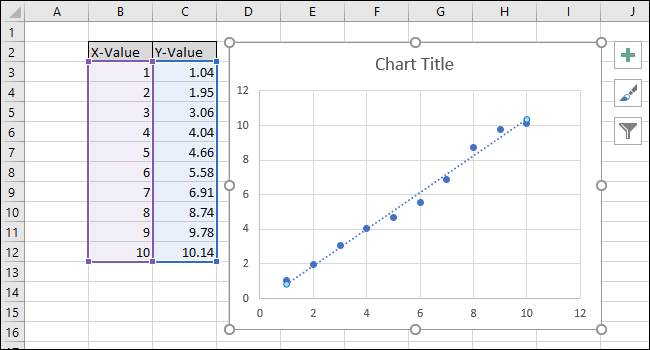
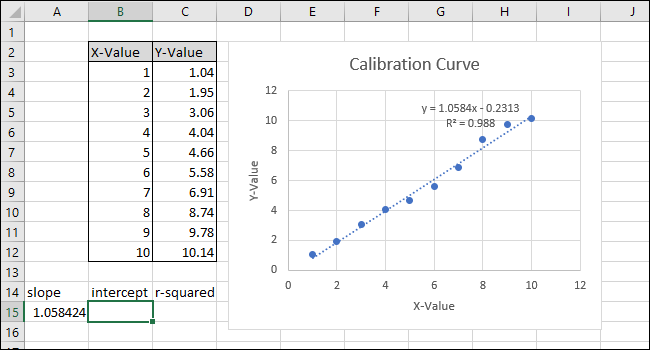
Menyn ”Formatera trendlinje” visas på höger sida av skärmen. Markera rutorna ”Visa ekvation i diagrammet” och ”Visa R-kvadratvärde i diagrammet”. R-kvadratvärdet är en statistisk måttenhet som anger hur väl linjen anpassar sig till datan. Det optimala R-kvadratvärdet är 1, vilket indikerar att alla datapunkter ligger direkt på linjen. Ju större skillnader mellan datapunkterna och linjen, desto lägre blir r-kvadratvärdet, med 0 som lägsta möjliga värde.
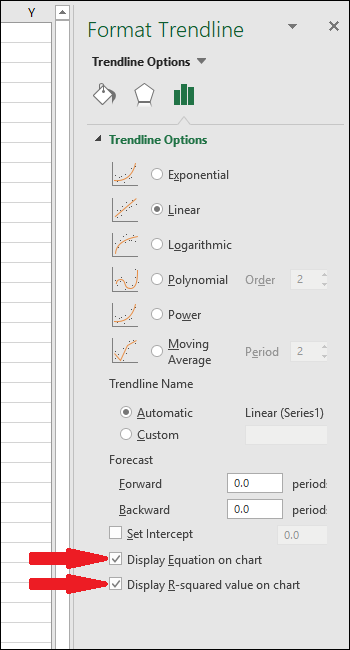
Ekvationen och R-kvadratvärdet för trendlinjen visas nu i diagrammet. I vårt exempel är korrelationen mycket stark, med ett R-kvadratvärde på 0,988.
Ekvationen är på formen ”Y = Mx + B”, där M representerar lutningen och B är linjens skärningspunkt med y-axeln.
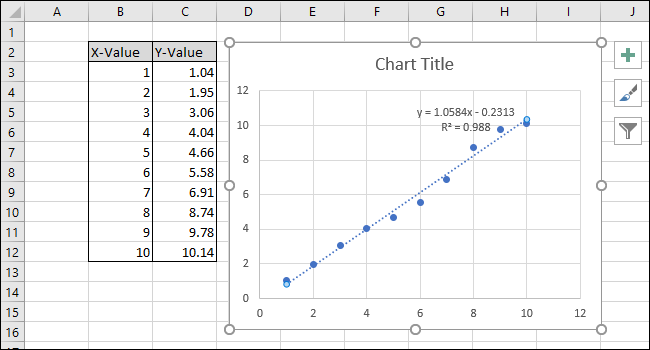
Nu när kalibreringen är färdigställd, kan vi anpassa diagrammet genom att redigera titeln och lägga till axeltitlar.
För att ändra diagrammets titel, klicka på den för att markera texten.
Skriv nu in en ny titel som beskriver diagrammets innehåll.
För att lägga till titlar till x-axeln och y-axeln, gå först till Diagramverktyg > Design.
Klicka på rullgardinsmenyn ”Lägg till diagramelement”.
Navigera nu till Axeltitlar > Primär horisontell.
En axeltitel visas.
För att ändra axeltitelns namn, markera texten och ange en ny titel.
Gå nu till Axeltitlar > Primär vertikal.
En ny axeltitel visas.
Ändra namn på titeln genom att markera texten och ange en ny titel.
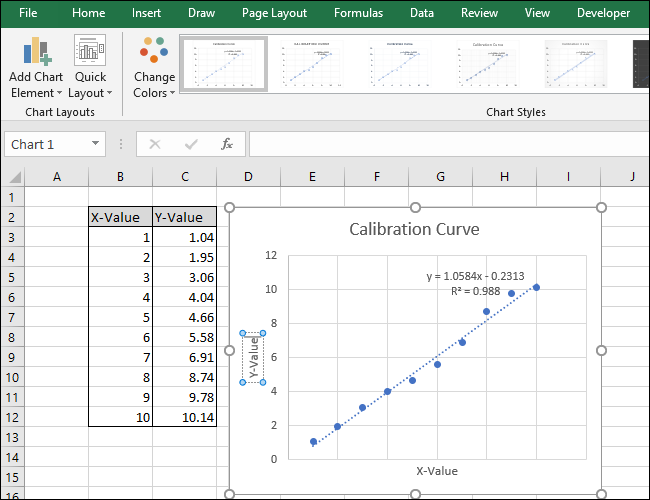
Ditt diagram är nu färdigt.
Steg två: Beräkna linjens ekvation och R-kvadratvärdet
Låt oss nu beräkna linjens ekvation och R-kvadratvärdet med Excels inbyggda funktioner SLUTTNING, SKÄRNING och KORREL.
Vi har lagt till rubriker för dessa tre funktioner i vårt kalkylblad (på rad 14). De faktiska beräkningarna kommer att ske i cellerna under rubrikerna.
Vi börjar med att beräkna SLUTTNING. Markera cell A15.
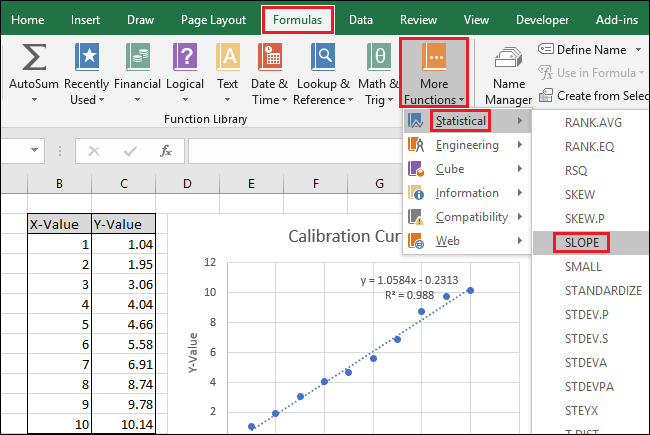
Navigera till Formler > Fler funktioner > Statistik > SLUTTNING.
Fönstret Funktionsargument visas. Markera eller ange cellerna i kolumnen ”Y-Värde” i fältet ”Kända_y”.
Markera eller ange cellerna i kolumnen ”X-Värde” i fältet ”Kända_x”. Ordningen på fälten ”Kända_y” och ”Kända_x” är avgörande för SLUTTNING-funktionen.
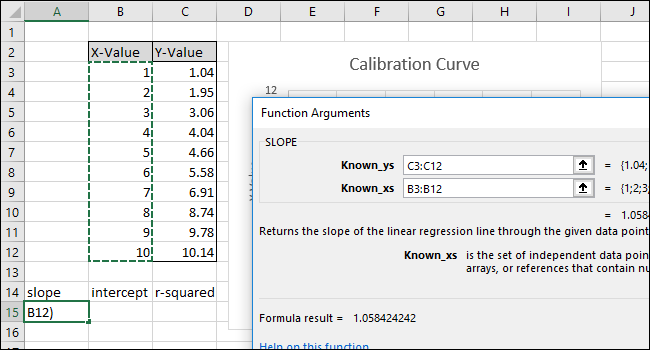
Klicka på ”OK”. Den slutgiltiga formeln i formelfältet bör se ut så här:
=SLUTTNING(C3:C12;B3:B12)
Observera att värdet som returneras av SLUTTNING-funktionen i cell A15 stämmer överens med värdet som visas i diagrammet.
Markera sedan cell B15 och gå till Formler > Fler funktioner > Statistik > SKÄRNING.
Fönstret Funktionsargument visas. Markera eller ange cellerna i kolumnen ”Y-Värde” för fältet ”Kända_y”.
Markera eller ange cellerna i kolumnen ”X-Värde” för fältet ”Kända_x”. Ordningen på fälten ”Kända_y” och ”Kända_x” är även här avgörande för SKÄRNING-funktionen.
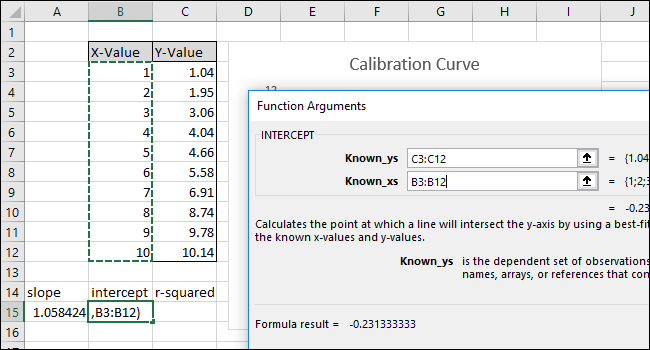
Klicka på ”OK”. Den slutgiltiga formeln i formelfältet bör se ut så här:
=SKÄRNING(C3:C12;B3:B12)
Observera att värdet som returneras av funktionen SKÄRNING stämmer överens med y-axelns skärningspunkt i diagrammet.
Markera sedan cell C15 och gå till Formler > Fler funktioner > Statistik > KORREL.
Fönstret Funktionsargument visas. Markera eller ange något av de två cellområdena för fältet ”Matris1”. Till skillnad från SLUTTNING och SKÄRNING påverkar ordningen inte resultatet av KORREL-funktionen.
Markera eller ange det andra av de två cellområdena för fältet ”Matris2”.
Klicka på ”OK”. Formeln i formelfältet bör se ut så här:
=KORREL(B3:B12;C3:C12)
Observera att värdet som returneras av KORREL-funktionen inte överensstämmer med det ”r-kvadrat”-värdet i diagrammet. KORREL-funktionen returnerar ”R”, så vi måste kvadrera det för att beräkna ”R-kvadrat”.
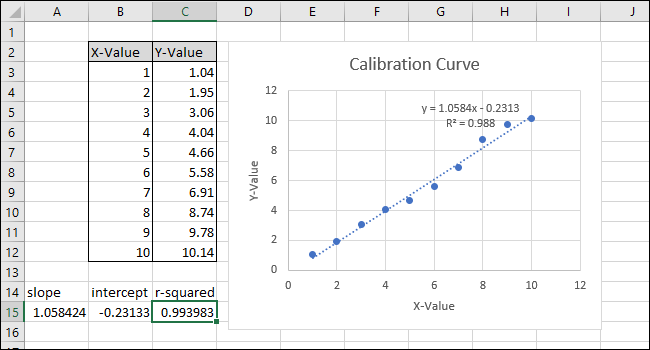
Klicka inuti funktionsfältet och lägg till ”^2” i slutet av formeln för att kvadrera värdet som returneras av KORREL-funktionen. Den färdiga formeln ska nu se ut så här:
=KORREL(B3:B12;C3:C12)^2
Tryck på Enter.
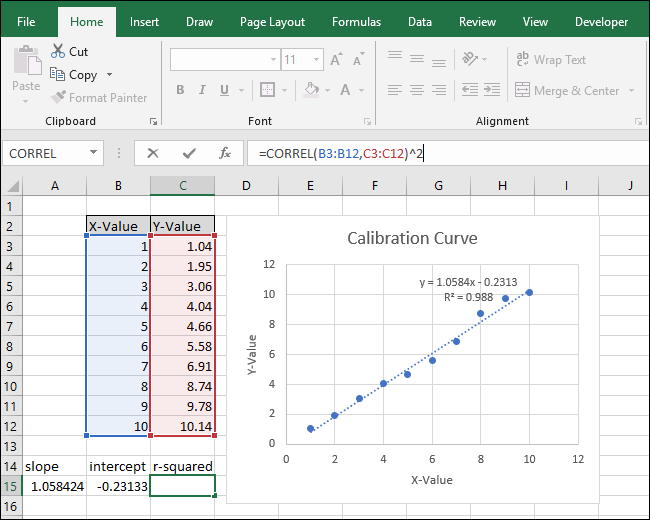
Efter att ha modifierat formeln stämmer nu ”R-kvadrat”-värdet överens med det som visas i diagrammet.
Steg tre: Konfigurera formler för snabb beräkning av värden
Nu kan vi använda dessa värden i enkla formler för att bestämma koncentrationen av den ”okända” lösningen, eller vilket inmatningsvärde vi ska ange i koden för att kulan ska flyga ett visst avstånd.
Dessa steg kommer att konfigurera de formler som krävs för att du ska kunna ange ett X-värde eller ett Y-värde och få motsvarande värde utifrån kalibreringskurvan.
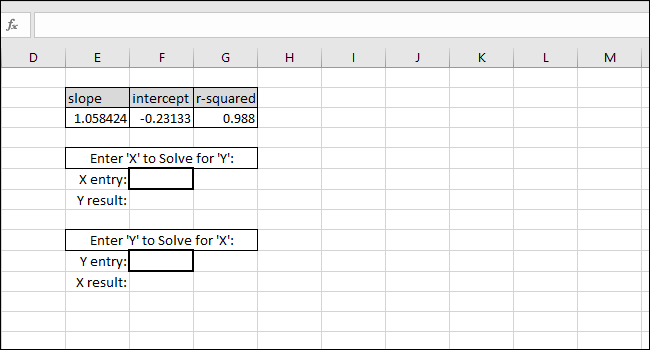
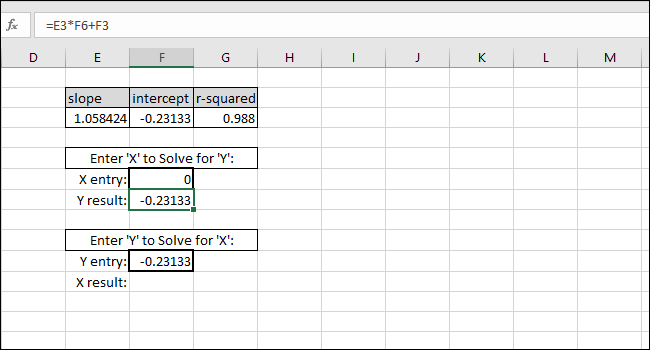
Ekvationen för den bäst anpassade linjen är av formen ”Y-värde = SLUTTNING * X-värde + SKÄRNING”. För att lösa för ”Y-värdet”, multiplicera X-värdet med SLUTTNING och lägg sedan till SKÄRNING.
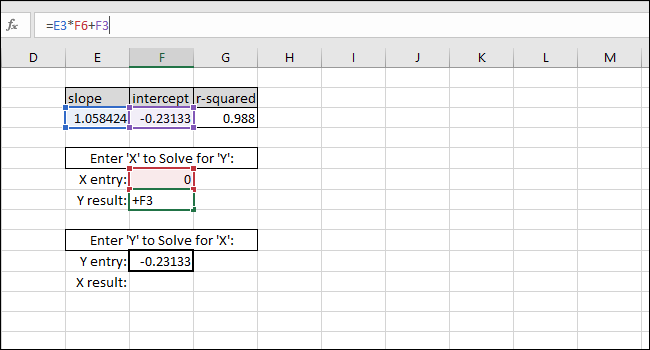
Som ett exempel anger vi noll som X-värde. Det Y-värde som returneras bör vara lika med SKÄRNING för den bäst anpassade linjen. Det stämmer, så vi vet att formeln fungerar som den ska.
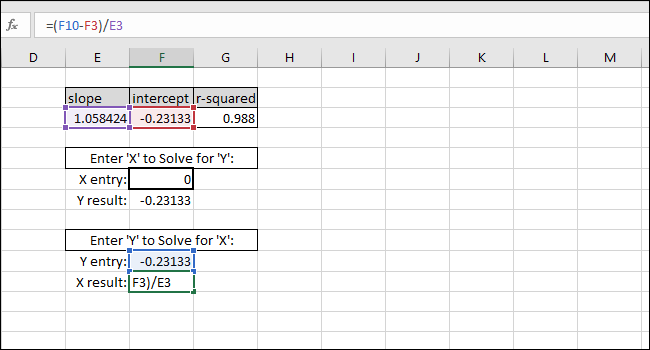
För att lösa ut X-värdet baserat på ett Y-värde, subtrahera SKÄRNING från Y-värdet och dela resultatet med SLUTTNING:
X-värde=(Y-värde-SKÄRNING)/SLUTTNING
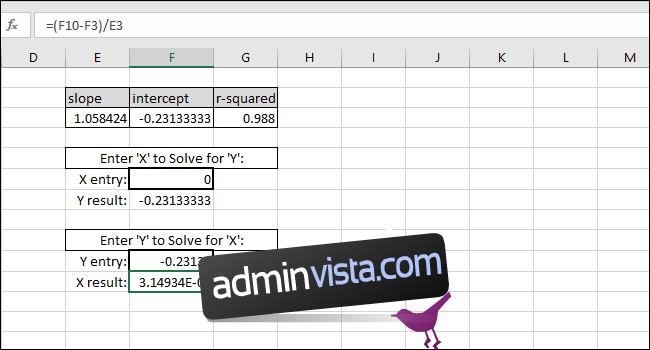
Som ett exempel har vi använt SKÄRNING som Y-värde. X-värdet som returneras bör vara noll, men värdet som returneras är 3,14934E-06. Det returnerade värdet är inte noll eftersom vi oavsiktligt trunkerade SKÄRNING-resultatet när vi skrev in värdet. Formeln fungerar dock korrekt eftersom resultatet är 0,00000314934, vilket i princip är noll.
Du kan ange valfritt X-värde i den första markerade cellen, och Excel kommer automatiskt att beräkna motsvarande Y-värde.
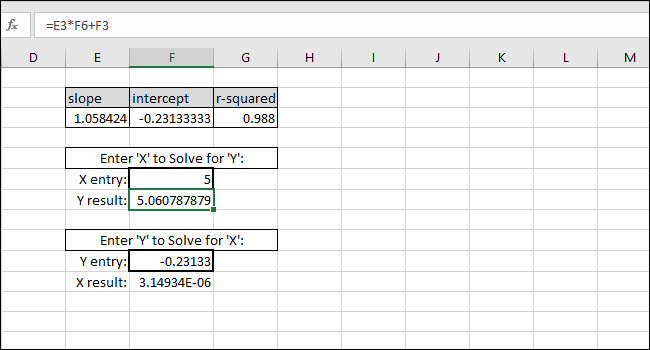
Om du anger ett valfritt Y-värde i den andra markerade cellen, får du motsvarande X-värde. Denna formel skulle du använda för att beräkna koncentrationen av en okänd lösning, eller det värde som behövs för att skicka en kula ett visst avstånd.
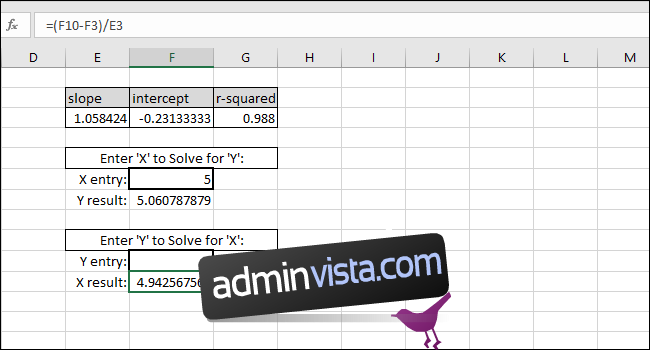
I detta exempel visar instrumentet ”5”, vilket enligt kalibreringen tyder på en koncentration på 4,94. Alternativt, om vi vill att kulan ska färdas fem enheter avstånd, föreslår kalibreringen att vi anger 4,94 som indatavariabel för programmet som styr kulkastaren. Vi kan vara ganska säkra på dessa resultat tack vare det höga R-kvadratvärdet i vårt exempel.