Ett Z-värde, eller Z-poäng, är ett statistiskt mått som indikerar hur många standardavvikelser en specifik datapunkt avviker från medelvärdet av en hel datamängd. För att beräkna detta används funktionerna AVERAGE och STDEV.S eller STDEV.P för att fastställa medelvärdet och standardavvikelsen, vilket sedan används för att beräkna Z-poängen för varje enskilt värde.
Vad innebär ett Z-värde och hur fungerar funktionerna AVERAGE, STDEV.S och STDEV.P?
En Z-poäng är ett praktiskt sätt att jämföra data från olika datamängder. Den representerar antalet standardavvikelser som en datapunkt ligger från medelvärdet. Den generella formeln för detta ser ut så här:
=(Datapunkt-MEDEL(Datamängd))/STDEV(Datamängd)
Låt oss ta ett exempel för att göra detta tydligare. Anta att vi vill jämföra testresultaten för två elever i algebra, som har blivit undervisade av olika lärare. Den ena eleven fick 95 % på slutprovet, medan den andra fick 87 %.
Vid första anblicken kan 95 % verka mer imponerande, men vad händer om läraren i den andra klassen gav ett svårare prov? Genom att beräkna Z-poängen för varje elevs resultat, baserat på medelresultatet i respektive klass och standardavvikelsen för resultaten i varje klass, kan vi göra en mer rättvis jämförelse. En jämförelse av Z-poängen kan avslöja att eleven med 87 % i själva verket presterade bättre i relation till sin klass än eleven med 95 % gjorde i relation till sin klass.
Det första statistiska värdet vi behöver är ”medelvärde”, och Excels funktion ”MEDEL” beräknar detta värde. Den summerar alla värden inom ett specificerat cellområde och delar summan med antalet celler som innehåller numeriska värden, samtidigt som den ignorerar tomma celler.
Det andra statistiska värdet vi behöver är ”standardavvikelse”, och Excel erbjuder två olika funktioner för att beräkna detta på lite olika sätt.
I tidigare versioner av Excel fanns endast funktionen ”STDEV”, som beräknar standardavvikelsen med antagandet att datan representerar ett ”prov” av en population. I Excel 2010 introducerades två funktioner för att beräkna standardavvikelsen:
STDEV.S: Denna funktion motsvarar den tidigare funktionen ”STDEV”. Den beräknar standardavvikelsen och antar att datan utgör ett urval från en större population. Ett sådant urval kan vara t.ex. de myggor som samlats in för en studie eller ett antal bilar som tagits ut för krocktester.
STDEV.P: Denna funktion beräknar standardavvikelsen utifrån antagandet att datan representerar hela populationen. En hel population skulle kunna vara alla myggor på jorden eller alla bilar i en specifik produktionsserie.
Valet mellan dessa två funktioner beror på den specifika datamängden. Skillnaden i resultat är vanligtvis liten, men resultatet av ”STDEV.P” kommer alltid att vara lägre än resultatet av ”STDEV.S” för samma datamängd. Att använda STDEV.S är ett mer konservativt tillvägagångssätt, då det antar en större variation i datan.
Låt oss illustrera med ett exempel
I vårt exempel kommer vi att använda två kolumner, ”Värden” och ”Z-poäng”, samt tre ”hjälpceller” för att lagra resultaten från funktionerna ”MEDEL”, ”STDEV.S” och ”STDEV.P”. Kolumnen ”Värden” innehåller tio slumpmässiga tal runt 500, och i kolumnen ”Z-poäng” kommer vi att beräkna Z-poängen med hjälp av informationen som lagrats i ”hjälpcellerna”.
Vi börjar med att beräkna medelvärdet av talen med funktionen ”MEDEL”. Markera den cell där resultatet ska sparas.
Skriv in följande formel och tryck enter – eller använd menyn ”Formler”.
=AVERAGE(E2:E13)
För att komma åt funktionen via menyn ”Formler”, klicka på rullgardinsmenyn ”Fler funktioner”, välj ”Statistisk” och sedan ”MEDEL”.
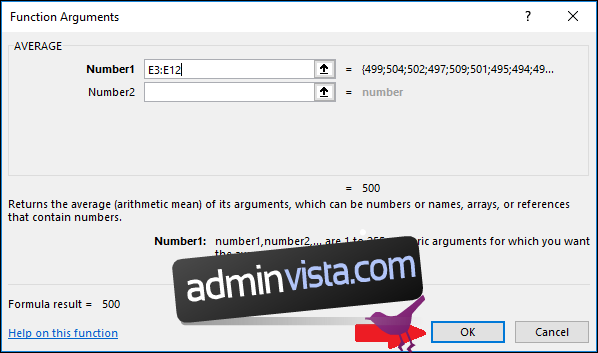
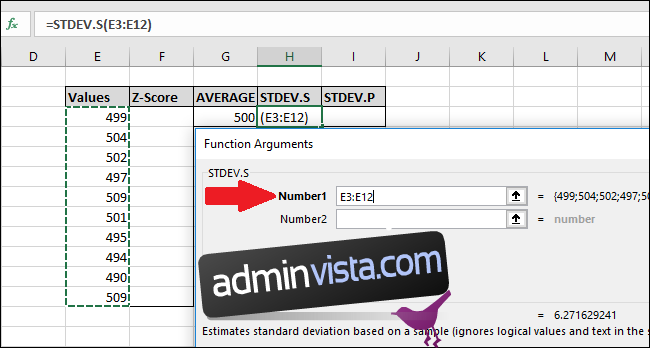
I fönstret Funktionsargument markerar du alla celler i kolumnen ”Värden” som indata för fältet ”Number1”. Fältet ”Number2” behöver inte fyllas i.
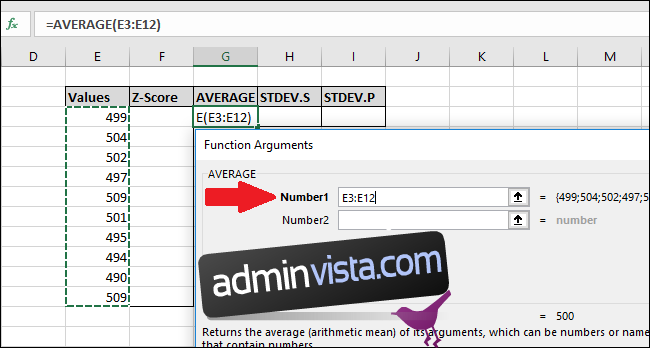
Klicka på ”OK”.
Nästa steg är att beräkna standardavvikelsen för värdena med antingen funktionen ”STDEV.S” eller ”STDEV.P”. I det här exemplet visar vi hur man beräknar båda, med början med ”STDEV.S”. Välj cellen där resultatet ska sparas.
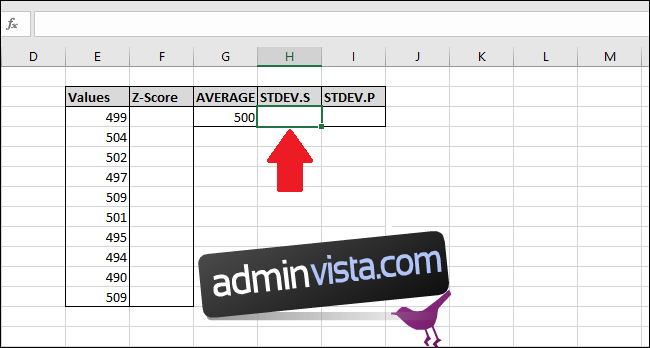
För att beräkna standardavvikelsen med ”STDEV.S”, skriv in följande formel och tryck enter (eller använd menyn ”Formler”).
=STDEV.S(E3:E12)
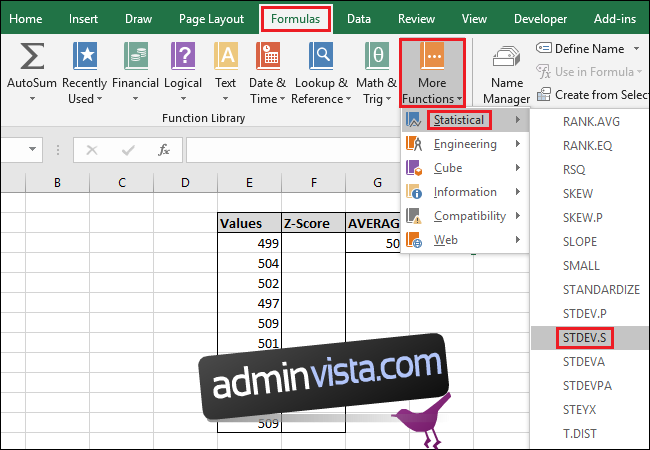
För att komma åt funktionen via menyn ”Formler”, klicka på rullgardinsmenyn ”Fler funktioner”, välj ”Statistisk”, scrolla ner och klicka på ”STDEV.S”.
I fönstret Funktionsargument markerar du alla celler i kolumnen ”Värden” som indata för fältet ”Number1”. ”Number2”-fältet behöver inte fyllas i.
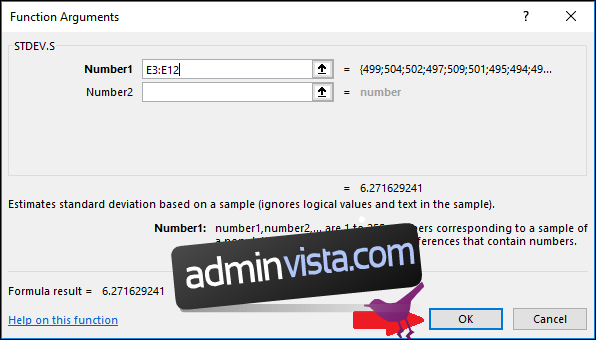
Klicka på ”OK”.
Nu beräknar vi standardavvikelsen med ”STDEV.P”. Välj cellen där resultatet ska sparas.
För att beräkna standardavvikelsen med ”STDEV.P”, skriv in följande formel och tryck enter (eller använd menyn ”Formler”).
=STDEV.P(E3:E12)
För att komma åt funktionen via menyn ”Formler”, klicka på rullgardinsmenyn ”Fler funktioner”, välj ”Statistisk”, scrolla ner och klicka på ”STDEV.P”.
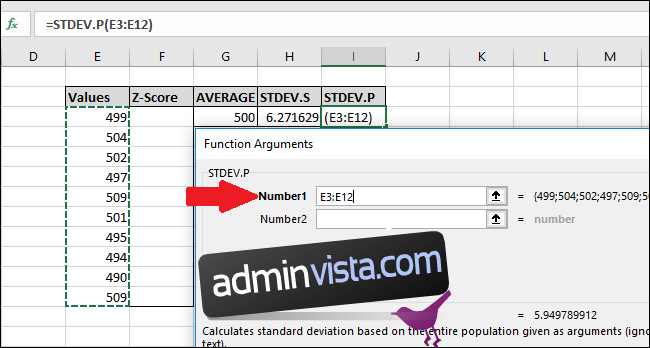
I fönstret Funktionsargument markerar du alla celler i kolumnen ”Värden” som indata för ”Number1”. ”Number2”-fältet lämnas tomt.
Klicka på ”OK”.
Nu när vi har medelvärdet och standardavvikelsen har vi allt som behövs för att beräkna Z-poängen. Vi använder en enkel formel som refererar till cellerna som innehåller resultaten från funktionerna ”MEDEL” och ”STDEV.S” eller ”STDEV.P”.
Välj den första cellen i kolumnen ”Z-poäng”. Vi använder resultatet från ”STDEV.S” i det här exemplet, men du kan lika gärna använda resultatet från ”STDEV.P”.
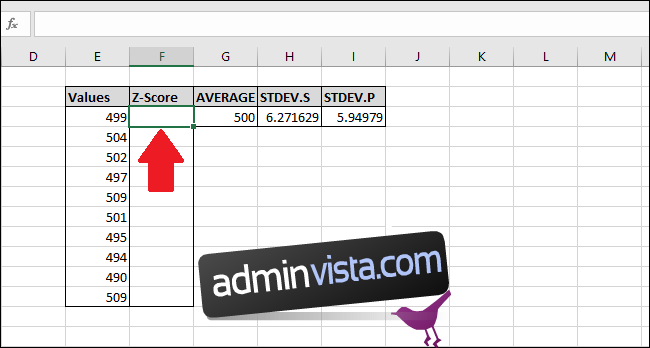
Skriv in följande formel och tryck enter:
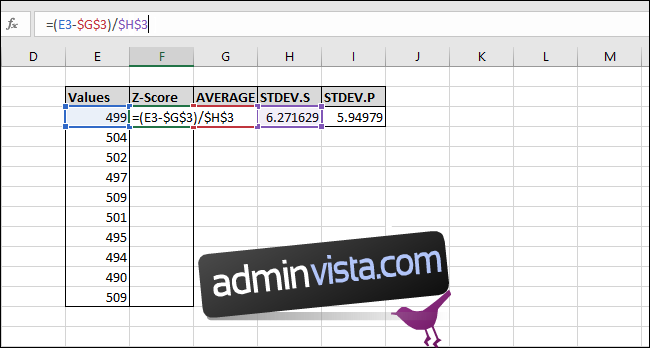
=(E3-$G$3)/$H$3
Alternativt kan du följa dessa steg för att skriva in formeln istället för att skriva direkt:
Klicka på cell F3 och skriv =(
Välj cell E3. (Du kan trycka på vänsterpil en gång eller använda musen)
Skriv minustecknet –
Välj cell G3 och tryck F4 för att lägga till ”$”-tecknen för att göra en ”absolut” cellreferens (det går igenom ”G3” > ”$G$3” > ”G$3” > ”$G3” > ”G3” om du trycker F4 flera gånger)
Skriv )/
Välj cell H3 (eller I3 om du använder ”STDEV.P”) och tryck F4 för att lägga till de två ”$”-tecknen.
Tryck enter
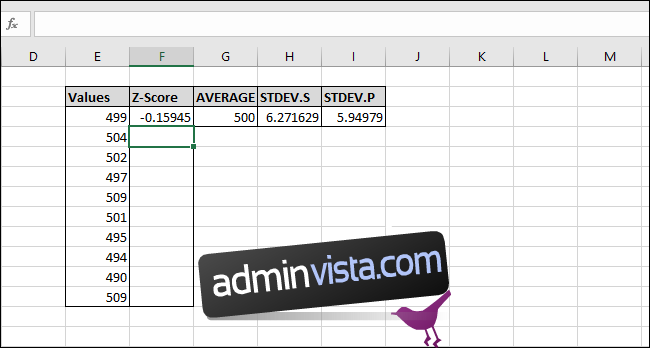
Z-poängen har nu beräknats för det första värdet, som ligger 0,15945 standardavvikelser under medelvärdet. För att verifiera resultatet kan du multiplicera standardavvikelsen med detta värde (6,271629 * -0,15945) och kontrollera att resultatet är samma som skillnaden mellan värdet och medelvärdet (499-500). Båda resultaten är identiska, så resultatet är korrekt.
Låt oss nu beräkna Z-poängen för resten av värdena. Markera hela kolumnen ”Z-poäng” från och med cellen som innehåller formeln.
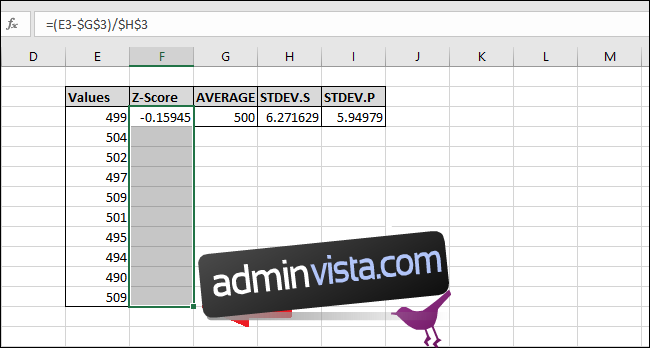
Tryck Ctrl+D, vilket kopierar formeln från den översta cellen ner till alla markerade celler.
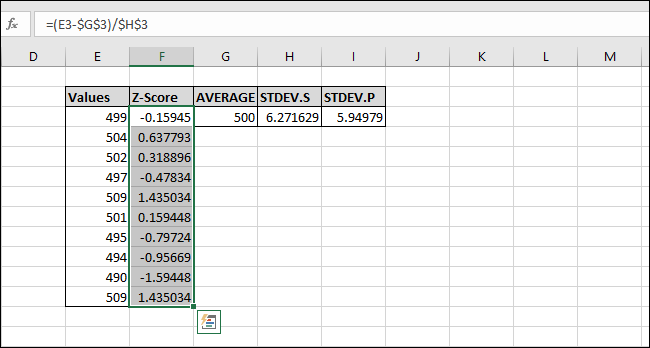
Formeln har nu applicerats på alla celler, och varje cell kommer alltid att referera till de korrekta ”MEDEL”- och ”STDEV.S”- eller ”STDEV.P”-cellerna tack vare ”$”-tecknen. Om du får fel, kontrollera att ”$”-tecknen är inkluderade i formeln.
Beräkna Z-poäng utan ”hjälpceller”
Hjälpceller lagrar ett resultat, som de som innehåller resultaten för funktionerna ”MEDEL”, ”STDEV.S” och ”STDEV.P”. De kan vara praktiska men är inte alltid nödvändiga. Du kan helt enkelt hoppa över dem när du beräknar Z-poäng genom att använda följande generaliserade formler istället.
Här är en formel som använder ”STDEV.S”:
=(Värde-MEDEL(Värden))/STDEV.S(Värden)
Och här är en som använder funktionen ”STEV.P”:
=(Värde-MEDEL(Värden))/STDEV.P(Värden)
När du anger cellområdena för ”Värden” i funktionerna, var noga med att använda absoluta referenser (”$” med F4) så att när du ”fyller ner”, beräknar du inte medelvärdet eller standardavvikelsen för ett annat område av celler i varje formel.
Om du har en stor datamängd kan det vara effektivare att använda hjälpceller eftersom de undviker att beräkna resultaten av ”MEDEL” och ”STDEV.S” eller ”STDEV.P” varje gång, vilket sparar processorresurser och minskar beräkningstiden.
Dessutom kräver ”$G$3” mindre lagringsutrymme och RAM än ”MEDEL($E$3:$E$12)”. Detta är viktigt eftersom standardversionen av 32-bitars Excel är begränsad till 2 GB RAM (64-bitarsversionen har inga sådana begränsningar).