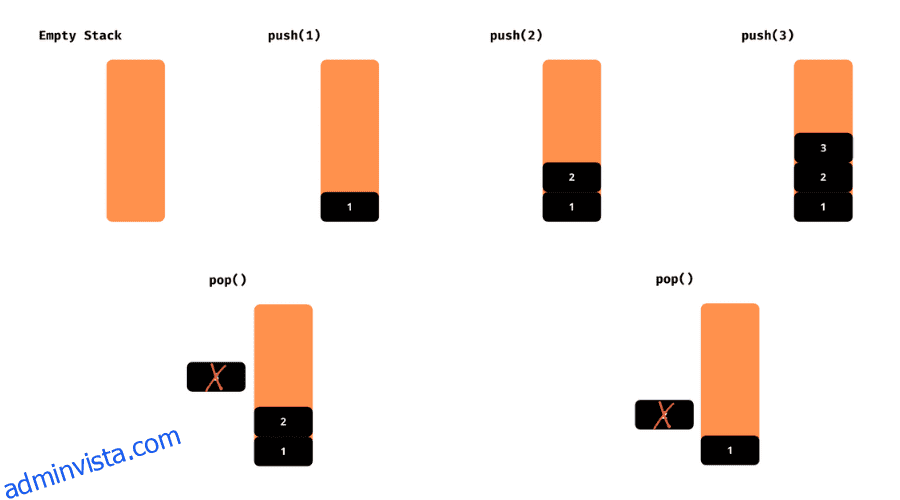Datastrukturer spelar en nyckelroll i programmeringsvärlden. De hjälper oss att organisera vår data på ett sätt som kan användas effektivt. Stacken är en av de enklaste datastrukturerna.
Låt oss lära oss om stacken och dess implementering i Python.
Innehållsförteckning
Vad är en stack?
En hög liknar högen med böcker, stolar, etc.., i verkligheten. Och den följer principen Last-in/First-out (LIFO). Det är den enklaste datastrukturen. Låt oss se scenariot med ett exempel från verkligheten.
Låt oss säga att vi har en hög med böcker enligt följande.
När vi vill ha den tredje boken från toppen då måste vi ta bort de två första böckerna från toppen för att ta ut den tredje boken. Här går den översta boken sist i högen och kommer först i högen. Datastrukturstacken följer samma princip Last-in/First-out (LIFO) vid programmering.
Operationer i Stack
Det finns huvudsakligen två operationer i en stack
1. push(data)
Lägger till eller skjuter in data i stacken.
2. pop()
Tar bort eller skjuter upp det översta elementet från stapeln.
Se nedanstående illustrationer av push- och pop-operationer.
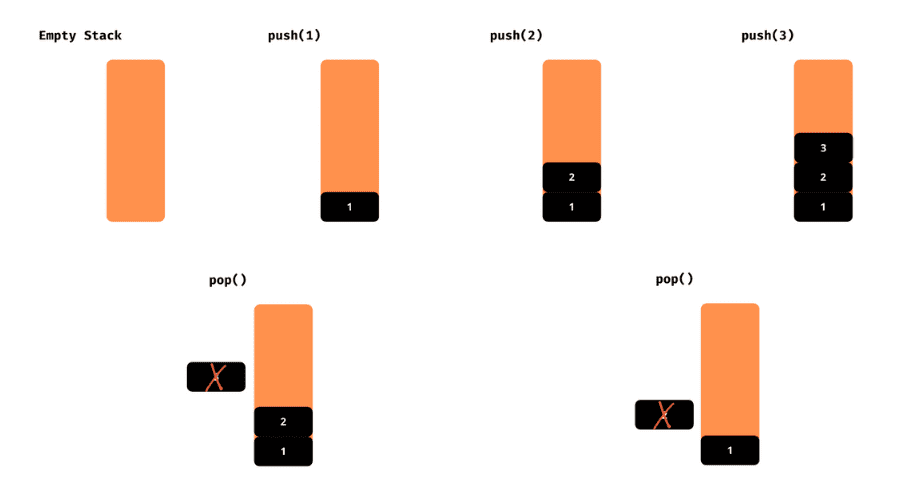
Vi kommer att skriva några hjälpfunktioner som hjälper oss att få mer info om stacken.
Låt oss se dem.
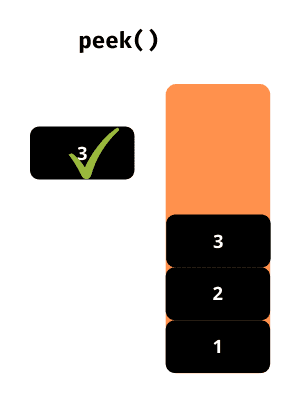
titt()
Returnerar det översta elementet från stacken.
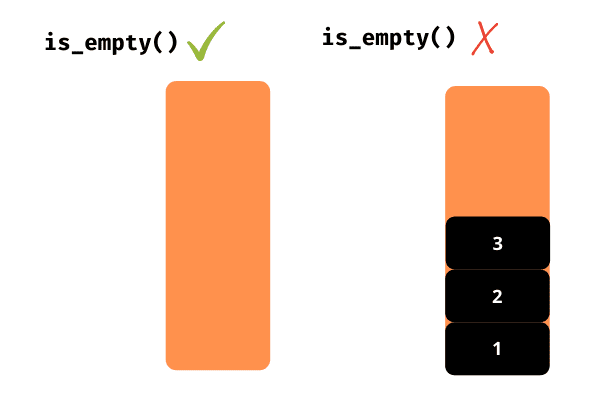
är tom()
Returnerar om stacken är tom eller inte.
Tillräckligt med konceptuella aspekter av stackdatastrukturen. Låt oss hoppa in i implementeringen utan vidare.
Jag antar att du har python installerat på din PC om inte kan du också prova onlinekompilatorn.
Stackimplementering
Att implementera stack är det enklaste jämfört med andra implementeringar av datastrukturer. Vi kan implementera en stack på flera sätt i Python.
Låt oss se dem alla en efter en.
#1. Lista
Vi ska implementera stacken med hjälp av listan i en klass. Låt oss se steg för steg implementeringen av stacken.
Steg 1: Skriv en klass som heter Stack.
class Stack: pass
Steg 2: Vi måste behålla data i en lista. Låt oss lägga till en tom lista i Stack-klassen med namnelement.
class Stack: def __init__(self): self.elements = []
Steg 3: För att trycka in elementen i stapeln behöver vi en metod. Låt oss skriva en push-metod som tar data som ett argument och lägger till den i elementlistan.
class Stack: def __init__(self): self.elements = [] def push(self, data): self.elements.append(data) return data
Steg 4: På samma sätt, låt oss skriva popmetoden som kommer ut det översta elementet från stacken. Vi kan använda popmetoden för listdatatypen.
class Stack: ## ... def pop(self): return self.elements.pop()
Vi har slutfört stackimplementeringen med nödvändiga operationer. Låt oss nu lägga till hjälpfunktionerna för att få mer information om stacken.
Steg 5: Vi kan få det översta elementet från stacken med det negativa indexet. Koden element[-1] returnerar den sista i listan. Det är det översta elementet i stacken i vårt fall.
class Stack: ## ... def peek(self): return self.elements[-1]
Steg 6: Om längden på elementlistan är 0, är stacken tom. Låt oss skriva en metod som returnerar om elementet är tomt eller inte.
class Stack: ## ... def is_empty(self): return len(self.elements) == 0
Vi har slutfört implementeringen av stacken med hjälp av listdatatypen.
åh! vänta vi har precis implementerat det. Men såg inte hur man använder den. Hur använder man den då?
Kom låt oss se hur man implementerar det. Vi måste skapa ett objekt för att Stack-klassen ska kunna använda det. Det är inte en stor sak. Låt oss göra det först.
class Stack:
## ...
if __name__ == '__main__':
stack = Stack()
Vi har skapat stackobjektet och är redo att använda det. Låt oss följa stegen nedan för att testa stackoperationer.
- Kontrollera om stacken är tom eller inte med metoden is_empty. Det bör returnera True.
- Tryck in siffrorna 1, 2, 3, 4, 5 i högen med push-metoden.
- Metoden is_empty bör returnera False. Kolla upp det.
- Skriv ut det översta elementet med tittmetoden.
- Poppa elementet från stapeln med popmetoden.
- Kontrollera kikelementet. Det bör returnera element 4.
- Ta nu alla element från stapeln.
- Metoden is_empty bör returnera True. Kolla upp det.
Vår stackimplementering är klar om den klarar alla ovanstående steg. Försök att skriva koden för stegen ovan.
Har du skrivit koden? Nej, oroa dig inte, kolla koden nedan.
class Stack:
def __init__(self):
self.elements = []
def push(self, data):
self.elements.append(data)
return data
def pop(self):
return self.elements.pop()
def peek(self):
return self.elements[-1]
def is_empty(self):
return len(self.elements) == 0
if __name__ == '__main__':
stack = Stack()
## checking is_empty method -> true
print(stack.is_empty())
## pushing the elements
stack.push(1)
stack.push(2)
stack.push(3)
stack.push(4)
stack.push(5)
## again checking is_empty method -> false
print(stack.is_empty())
## printing the topmost element of the stack -> 5
print(stack.peek())
## popping the topmost element -> 5
stack.pop()
## checking the topmost element using peek method -> 4
print(stack.peek())
## popping all the elements
stack.pop()
stack.pop()
stack.pop()
stack.pop()
## checking the is_empty method for the last time -> true
print(stack.is_empty())
hurra! vi har slutfört stackimplementeringen från början med hjälp av listdatatypen. Du kommer att se utdata som nämns nedan om du kör ovanstående kod.
True False 5 4 True
Vi kan direkt använda listdatatypen som en stack. Ovanstående implementering av stack hjälper dig att förstå stackimplementeringen även i andra programmeringsspråk.
Du kan också kolla in dessa listrelaterade artiklar.
Låt oss se den inbyggda dequen från samlingens inbyggda modul som kan fungera som en stack.
#2. deque från samlingar
Den är implementerad som en dubbelkö. Eftersom det stöder tillägg och borttagning av element från båda ändarna. Därför kan vi använda den som en stack. Vi kan få den att följa stackens LIFO-princip.
Den implementeras med hjälp av andra datastrukturer som kallas den dubbellänkade listan. Så prestandan för infogning och borttagning av element är konsekvent. Att komma åt element från den mittersta länkade listan tog O(n) tid. Vi kan använda den som en stack eftersom det inte finns något behov av att komma åt mittelementen från stapeln.
Innan du implementerar stacken, låt oss se metoderna som används för att implementera stacken med hjälp av kön.
- append(data) – används för att skicka data till stacken
- pop() – används för att ta bort det översta elementet från stacken
Det finns inga alternativa metoder för peek och is_empty. Vi kan skriva ut hela stapeln i stället för tittmetoden. Därefter kan vi använda len-metoden för att kontrollera om stacken är tom eller inte.
Låt oss implementera stacken med hjälp av deque från samlingsmodulen.
from collections import deque ## creating deque object stack = deque() ## checking whether stack is empty or not -> true print(len(stack) == 0) ## pushing the elements stack.append(1) stack.append(2) stack.append(3) stack.append(4) stack.append(5) ## again checking whether stack is empty or not -> false print(len(stack) == 0) ## printing the stack print(stack) ## popping the topmost element -> 5 stack.pop() ## printing the stack print(stack) ## popping all the elements stack.pop() stack.pop() stack.pop() stack.pop() ## checking the whether stack is empty or not for the last time -> true print(len(stack) == 0)
Det är allt. Vi har lärt oss hur man implementerar stack med hjälp av deque från samlingens inbyggda modul. Du kommer att få utdata enligt nedan om du kör programmet ovan.
True False deque([1, 2, 3, 4, 5]) deque([1, 2, 3, 4]) True
Hittills har vi sett två sätt att implementera stacken. Finns det några andra sätt att implementera en stack? Ja! Låt oss se det sista sättet att implementera en stack i denna handledning.
#3. LifoQueue
Själva namnet LifoQueue säger att det följer LIFO-principen. Därför kan vi använda den som en stack utan tvekan. Det är från den inbyggda modulkön. LifoQueue tillhandahåller några praktiska metoder som är användbara i stackimplementeringen. Låt oss se dem
- put(data) – lägger till eller skickar data till kön
- get() – tar bort eller poppar det översta elementet från kön
- empty() – returnerar om stacken är tom eller inte
- qsize() – returnerar längden på kön
Låt oss implementera stacken med LifoQueue från kömodulen.
from queue import LifoQueue
## creating LifoQueue object
stack = LifoQueue()
## checking whether stack is empty or not -> true
print(stack.empty())
## pushing the elements
stack.put(1)
stack.put(2)
stack.put(3)
stack.put(4)
stack.put(5)
## again checking whether stack is empty or not -> false
print(stack.empty())
## popping all the elements
print(stack.get())
print(stack.get())
print(stack.get())
## checking the stack size
print("Size", stack.qsize())
print(stack.get())
print(stack.get())
## checking the whether stack is empty or not for the last time -> true
print(stack.empty())
Du kommer att få utdata som nämns nedan om du kör programmet ovan utan att ändra det.
True False 5 4 3 Size 2 2 1 True
Tillämpning av Stack
Nu har du tillräcklig kunskap om stackar för att tillämpa det i programmeringsproblem. Låt oss se ett problem och lösa det med en stack.
Givet ett uttryck, skriv ett program för att kontrollera om parenteser, hängslen, hängslen är korrekt balanserade eller inte.
Låt oss se några exempel.
Inmatning: ”[{}]([])”
Utgång: Balanserad
Inmatning: ”{[}]([])”
Utgång: Ej balanserad
Vi kan använda stacken för att lösa ovanstående problem. Låt oss se stegen för att lösa problemet.
- Skapa en stack för att lagra karaktärerna.
- Om längden på uttrycket är udda, är uttrycket inte balanserat
- Iterera genom det givna uttrycket.
- Om det aktuella tecknet är den inledande parentesen från ( eller { eller [, then push it to stack.
- Else if the current character is a closing bracket ) or } or ]hoppa sedan ur högen.
- Om det poppade tecknet stämmer överens med startparentesen, fortsätt annars är inte parenteser balanserade.
- Efter iterationen, om stacken är tom är ekvationen Balanserad, annars är ekvationen inte balanserad.
Vi kan använda den inställda datatypen för att kontrollera parantes matchning.
## stack
class Stack:
def __init__(self):
self.elements = []
def push(self, data):
self.elements.append(data)
return data
def pop(self):
return self.elements.pop()
def peek(self):
return self.elements[-1]
def is_empty(self):
return len(self.elements) == 0
def balance_check(expression):
## checking the length of the expression
if len(expression) % 2 != 0:
## not balanced if the length is odd
return False
## for checking
opening_brackets = set('([{')
pairs = set([ ('(',')'), ('[',']'), ('{','}') ])
## stack initialization
stack = Stack()
## iterating through the given expression
for bracket in expression:
## checking whether the current bracket is opened or not
if bracket in opening_brackets:
## adding to the stack
stack.push(bracket)
else:
## popping out the last bracket from the stack
popped_bracket = stack.pop()
## checking whether popped and current bracket pair
if (popped_bracket, bracket) not in pairs:
return False
return stack.is_empty()
if __name__ == '__main__':
if balance_check('[{}]([])'):
print("Balanced")
else:
print("Not Balanced")
if balance_check('{[}]([])'):
print("Balanced")
else:
print("Not Balanced")
Vi kan använda stacken för att lösa många fler problem. Ovanstående problem är ett av dem. Försök att tillämpa stackkonceptet där du tycker att det passar dig bäst.
Slutsats
Jaha! Du har slutfört handledningen. Jag hoppas att du tyckte om handledningen lika mycket som jag när du gjorde den. Det var allt för handledningen.
Glad kodning 🙂 👨💻