Sökalgoritmer implementeringar i Python

Att utveckla en söklösning kan vara en utmaning, men absolut inte omöjligt.

I praktiken söker vi oftast utan ett bestämt mönster. Vi letar helt enkelt på de ställen där vi tror att det vi söker kan finnas. Vi följer sällan en strukturerad metod.

Men fungerar det på samma sätt inom programmering?

Nej, inom programmering krävs det ofta ett mönster eller en algoritm för att effektivt söka efter information. I den här artikeln kommer vi att utforska några av de algoritmer som används för sökning och som följer olika metoder.

Det finns ett flertal algoritmer tillgängliga inom programmering. Vi kommer att fokusera på de mest centrala och frekvent använda i den här genomgången. När du har bekantat dig med dessa kommer de övriga att bli enklare att förstå.

I denna artikel avser sökning processen att lokalisera ett specifikt element inom en array.

Låt oss undersöka dessa algoritmer en i taget.

Linjär Sökning

Som namnet antyder, följer linjärsökningsalgoritmen ett linjärt tillvägagångssätt när den söker efter element i en array. Algoritmen startar sökningen från början av arrayen och fortsätter systematiskt till slutet, tills det önskade elementet påträffas. Programmet avbryter sökningen när elementet har hittats.

För att underlätta förståelsen av algoritmen, låt oss illustrera linjärsökning med några exempel.

Genom att noggrant studera sökprocessen kommer du att märka att den tid som krävs för att genomföra programmet i värsta fall är O(n). Vid analys av algoritmer bör vi beakta den maximala tidsåtgången som kan krävas. Därför är tidskomplexiteten för denna algoritm O(n).

Låt oss nu granska implementeringen av linjärsökning.

Implementering av Linjär Sökning

Nu har du en god förståelse för hur linjärsökning fungerar. Det är dags att koda. Låt oss först bryta ner de steg som krävs för att implementera algoritmen. Därefter kan du försöka skriva koden själv. Om det inte går direkt, oroa dig inte; jag kommer att tillhandahålla den fullständiga koden.

Följande är stegen för att implementera linjärsökning:

• Initiera en array med önskade element (dina favoritnummer).
• Skapa en funktion, till exempel ”sok_element”, som tar tre parametrar: arrayen, arrayens längd och elementet som ska sökas.
• sok_element(arr, n, element):
  • Gå igenom arrayen element för element.
    • Kontrollera om det nuvarande elementet överensstämmer med det sökta elementet.
    • Om det gör det, returnera True.
  • Om loopen avslutas utan att hitta elementet, betyder det att elementet inte finns i arrayen. Returnera False.
• Skriv ut ett meddelande som indikerar om funktionen ”sok_element” returnerade True eller False.

Använd ovanstående steg för att skriva koden för linjärsökning.

Har du lyckats implementera algoritmen? Jag hoppas det. Om du har det, jämför din kod med följande exempel.

Om du inte lyckades, oroa dig inte. Granska koden nedan och studera hur den har implementerats. Med lite övning kommer du snart att bemästra det.

## Sökfunktion
def sok_element(arr, n, element):
    ## Iterera genom arrayen
    for i in range(n):
        ## Kontrollera om det aktuella elementet matchar det sökta elementet
        if arr[i] == element:
            ## Returnera True vid matchning
            return True
    ## Elementet hittades inte, därför avslutas funktionen här
    return False
if __name__ == '__main__':
    ## Initiera array, längd och element som ska sökas
    arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    n = 10
    element_att_soka = 6
    # element_att_soka = 11
    if sok_element(arr, n, element_att_soka):
        print(element_att_soka, "hittades")
    else:
        print(element_att_soka, "hittades inte")

Testa programmet först med ett element som finns i arrayen och sedan med ett som inte gör det.

Tidskomplexiteten för linjärsökning är O(n).

Kan vi förbättra effektiviteten med hjälp av andra metoder?

Ja, det kan vi. Låt oss se hur.

Binär Sökning

Binärsökning undersöker alltid det mittersta elementet i arrayen. Denna algoritm används endast på sorterade arrays.

Algoritmen itererar genom arrayen, kontrollerar det mellersta elementet och avslutar om matchning hittas. Om det mellersta elementet är mindre än det sökta elementet, utesluts den vänstra halvan av arrayen från sökningen. Om det mittersta elementet är större, utesluts den högra halvan.

Vid varje iteration reducerar binärsökning det område som ska genomsökas, vilket resulterar i färre kontroller jämfört med linjärsökning.

Följande illustrationer kan hjälpa dig att bättre förstå hur algoritmen fungerar.

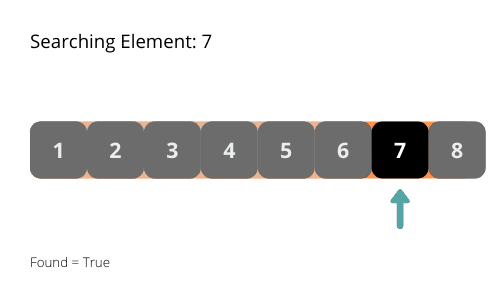
Tidskomplexiteten för binärsökning är O(log n). Vid varje iteration halveras sökutrymmet, vilket innebär att sökningen går exponentiellt snabbare.

Implementering av Binär Sökning

Låt oss först gå igenom stegen och sedan presentera koden. Stegen för implementering av binärsökning är:

• Initiera arrayen med element (dina lyckonummer).
• Skapa en funktion, till exempel ”sok_element”, som tar tre parametrar: den sorterade arrayen, arrayens längd och elementet som ska sökas.
• sok_element(sorterad_arr, n, element):
  • Initiera ett index för att gå igenom arrayen.
  • Initiera två variabler som anger start- och slutindexen för sökområdet.
  • Fortsätt iterera så länge indexet är mindre än arrayens längd.
    • Beräkna mittindexet i sökområdet med hjälp av start- och slutindexen: (start + slut) // 2.
    • Kontrollera om elementet vid mittindexet är lika med det sökta elementet.
    • Om det matchar, returnera True.
    • Om elementet vid mittindexet är mindre än det sökta elementet, flytta fram startindexet till mitten + 1.
    • Om elementet vid mittindexet är större än det sökta elementet, flytta bak slutindexet till mitten – 1.
    • Öka arrayindexet.
  • Om loopen slutförts utan att hitta elementet, returnera False.
• Skriv ut ett meddelande som visar resultatet av sökningen.

Försök skriva koden, likt implementeringen av linjärsökning.

…

Har du lyckats skapa koden?

Om du har det, jämför den med koden nedan. Om inte, ta en titt på koden för att förstå implementeringen.

## Sökfunktion
def sok_element(sorterad_arr, n, element):
    ## Array-index för iteration
    i = 0
    ## Variabler för att hantera sökområdet
    ## Initierar med start- och slutindex
    start = 0
    end = n - 1
    ## Iterera genom arrayen
    while i < n:
        ## Hämta index för det mittersta elementet
        middle = (start + end) // 2
        ## Kontrollera om det mittersta elementet matchar det sökta elementet
        if sorterad_arr[middle] == element:
            ## Returnera True om elementet finns i arrayen
            return True
        elif sorterad_arr[middle] < element:
            ## Flytta startindexet för sökområdet till höger
            start = middle + 1
        else:
            ## Flytta slutindexet för sökområdet till vänster
            end = middle - 1
        i += 1
    return False
if __name__ == '__main__':
    ## Initiera array, längd och element att söka efter
    arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    n = 10
    element_att_soka = 9
    # element_att_soka = 11
    if sok_element(arr, n, element_att_soka):
        print(element_att_soka, "hittades")
    else:
        print(element_att_soka, "hittades inte")

Testa koden i olika scenarier, både med element som finns i arrayen och de som inte gör det.

Slutsats

Binärsökning är betydligt effektivare än linjärsökning. Dock krävs att arrayen är sorterad för att använda binärsökning, vilket inte är nödvändigt för linjärsökning. Sorteringen tar lite tid, men användningen av effektiva sorteringsalgoritmer kan ge en bra kombination med binärsökning.

Nu har du bra kunskaper om några av de mest använda sökalgoritmerna i Python.

Utforska gärna några populära open-source sökmotorer.

Lycka till med kodningen! 🙂 🧑‍💻