Hur man skriver ut Pascals triangel i Python

Innehållsförteckning

Denna guide kommer att visa dig hur du genererar och visar Pascals triangel i Python, baserat på ett specifikt antal rader.

Vi börjar med att utforska hur Pascals triangel är uppbyggd. Därefter går vi vidare till att skapa en Python-funktion för detta, samt undersöka optimeringsmöjligheter.

▶️ Låt oss sätta igång!

Vad är Pascals triangel och hur konstrueras den?

Att generera Pascals triangel med ett angivet antal rader är en vanlig uppgift i programmeringsintervjuer.

I Pascals triangel med ’n’ rader, har rad nummer ’i’, ’i’ element.

Den första raden innehåller endast ett element, vilket är ’1’. Varje efterföljande elements värde är summan av de två elementen direkt ovanför det i föregående rad.

Illustrationen nedan visar konstruktionen av Pascals triangel med fem rader.

Notera att nollor kan betraktas som osynliga element när vi endast har en siffra ovanför ett specifikt element.

📝Som en snabb övning, försök att konstruera Pascals triangel för ’n=6’ och ’n=7’ enligt ovanstående metod.

Låt oss nu börja koda. Du kan använda adminvista.coms Python IDE direkt i webbläsaren när du arbetar igenom denna handledning.

Python-funktion för att visa Pascals triangel

I detta avsnitt ska vi skapa en Python-funktion som visar Pascals triangel för ett givet antal rader.

Det finns två viktiga aspekter att beakta:

Hur representeras elementen i Pascals triangel matematiskt?
Hur visas Pascals triangel med korrekt avstånd och formatering?

Låt oss besvara dessa frågor.

#1. Hur uttrycker vi varje element i Pascals triangel?

Det visar sig att elementen i Pascals triangel kan beräknas med formeln för nCr. Om du minns matematiken från skolan, representerar nCr antalet sätt att välja ’r’ objekt från en mängd av ’n’ objekt.

Formeln för nCr är som följer:

Låt oss nu använda nCr-formeln för att uttrycka elementen i Pascals triangel.

Vi har nu ett sätt att representera elementen i triangeln.

#2. Hur hanterar vi avståndet när vi visar mönstret?

I Pascals triangel med ’numRows’ rader, har rad #1 ett element, rad #2 har två element, och så vidare. För att visa triangeln korrekt behöver vi ’numRows – i’ mellanslag på rad #i. Vi kan använda Pythons ’range’-funktion tillsammans med en ’for’-loop för att åstadkomma detta.

Eftersom ’range’-funktionen utesluter slutpunkten som standard, måste vi lägga till +1 för att få det korrekta antalet inledande mellanslag.

Nu när vi vet hur elementen representeras och hur avståndet hanteras, låt oss definiera funktionen ’pascal_tri’.

Analysera funktionsdefinitionen

Vad ska funktionen ’pascal_tri’ göra?

Funktionen ’pascal_tri’ ska ta antalet rader (’numRows’) som argument.
Den ska visa Pascals triangel med ’numRows’ rader.

För att beräkna fakulteten, låt oss använda ’factorial’-funktionen från Pythons inbyggda matematikmodul.

▶️ Kör följande kod för att importera ’factorial’ och använda den i den aktuella modulen.

from math import factorial

Kodavsnittet nedan visar funktionsdefinitionen.

def pascal_tri(numRows):
  '''Visar Pascals triangel med numRows.'''
  for i in range(numRows):
    # Loop för att skapa inledande mellanslag
    for j in range(numRows-i):
      print(end=" ")
    
    # Loop för att beräkna element i rad i
    for j in range(i+1):
      # nCr = n!/((n-r)!*r!)
      print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")

    # Visa varje rad på en ny linje
    print("n")

Funktionen fungerar på följande sätt:

Funktionen ’pascal_tri’ tar en obligatorisk parameter ’numRows’: antalet rader.
Det finns totalt ’numRows’ rader. För varje rad ’i’ lägger vi till ’numRows – i’ inledande mellanslag före det första elementet i raden.
Vi använder sedan nCr-formeln för att beräkna varje enskilt element. För rad ’i’ är elementen iCj där j = {0,1,2,..,i}.
Vi använder ’//’ för att utföra heltalsdivision eftersom vi vill att elementen ska vara heltal.
Efter att ha beräknat alla element i en rad, skriver vi ut nästa rad på en ny linje.

🔗 Eftersom vi har lagt till en docstring, kan vi använda Pythons inbyggda ’help’-funktion eller attributet ’__doc__’ för att få tillgång till dokumentationen för funktionen. Kodavsnittet nedan visar hur du gör.

help(pascal_tri)

# Utdata
# Hjälp om funktionen pascal_tri i modulen __main__:
# pascal_tri(numRows)
#     Visar Pascals triangel med numRows.

# pascal_tri.__doc__

# Utdata
# 'Visar Pascals triangel med numRows.'

Låt oss nu anropa funktionen med antalet rader som argument.

pascal_tri(3)

# Utdata
     1
    1 1
   1 2 1

De första 3 raderna av Pascals triangel visas som förväntat.

Visa Pascals triangel med rekursion

I föregående avsnitt identifierade vi det matematiska uttrycket för varje element i Pascals triangel. Vi utnyttjade däremot inte sambandet mellan element i två efterföljande rader.

Vi använde ju föregående rad för att beräkna elementen i nästa rad. Kan vi använda detta för en rekursiv implementering av funktionen ’pascal_tri’?

Absolut, låt oss göra det!

I en rekursiv implementering anropar en funktion sig själv upprepade gånger tills basfallet uppnås. I konstruktionen av Pascals triangel startar vi med den första raden med elementet 1 och bygger sedan efterföljande rader.

Funktionsanropet ’pascal_tri(numRows)’ anropar i sin tur ’pascal_tri(numRows-1)’ och så vidare, tills basfallet ’pascal_tri(1)’ nås.

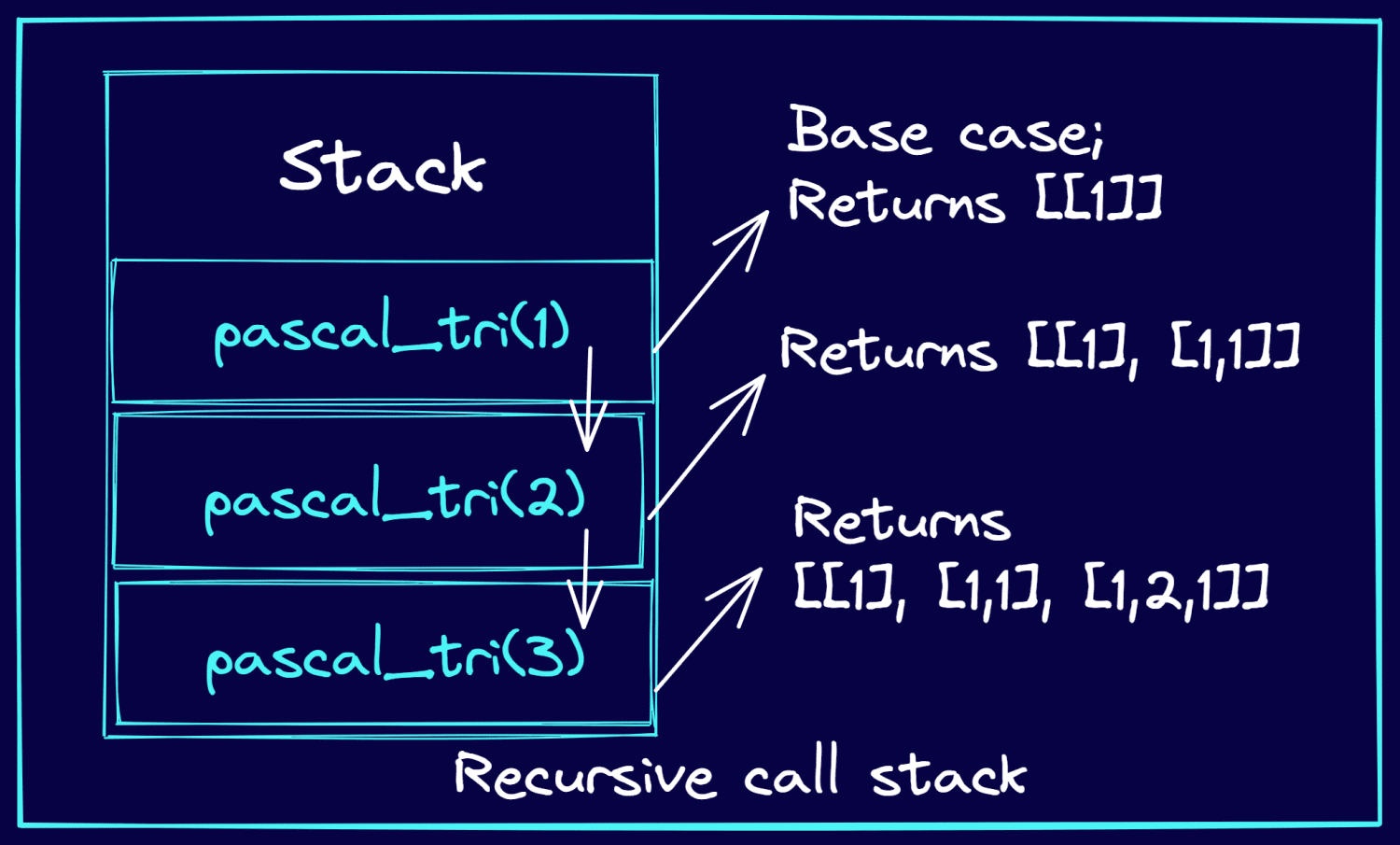
Tänk på exemplet där vi ska visa de första 3 raderna av Pascals triangel. Bilden nedan förklarar hur de rekursiva anropen läggs på stacken och hur de rekursiva funktionsanropen returnerar raderna i Pascals triangel.

▶️ Kör kodavsnittet nedan för att generera raderna i Pascals triangel rekursivt.

def pascal_tri(numRows):
    '''Visar Pascals triangel med numRows.'''
    if numRows == 1:
        return [[1]] # Basfallet är nått!
    else:
        res_arr = pascal_tri(numRows-1) # Rekursivt anrop till pascal_tri
        # Använd föregående rad för att beräkna den aktuella raden
        cur_row = [1] # Varje rad börjar med 1
        prev_row = res_arr[-1]
        for i in range(len(prev_row)-1):
            # Summan av de 2 elementen direkt ovanför
            cur_row.append(prev_row[i] + prev_row[i+1])
        cur_row += [1] # Varje rad slutar med 1
        res_arr.append(cur_row)
        return res_arr

Här är några viktiga punkter att notera:

Vi har använt en nästlad lista som datastruktur, där varje rad i Pascals triangel är en egen lista, så här: [[rad 1], [rad 2],…,[rad n]].
Funktionsanropet ’pascal_tri(numRows)’ triggar en serie rekursiva anrop med ’numRows – 1’, ’numRows – 2’ ända ner till 1 som argument. Dessa anrop läggs på en stack.
När ’numRows == 1’ har vi nått basfallet, och funktionen returnerar ’[[1]]’.
Den returnerade listan används sedan av de efterföljande funktionerna i anropsstacken för att beräkna nästa rad.
Om ’cur_row’ är den aktuella raden, så är ’cur_row[i] = prev_row[i] + prev_row[i+1]’ – summan av 2 element direkt ovanför det aktuella indexet.

Eftersom den returnerade arrayen är en nästlad lista (lista med listor), måste vi justera avståndet och visa elementen, som visas i kodavsnittet nedan.

tri_array = pascal_tri(5)

for i,row in enumerate(tri_array):
  for j in range(len(tri_array) - i):
    print(end=" ") # Inledande mellanslag
  for j in row:
    print(j, end=" ") # Visa element
  print("n")  # Ny rad

Utdata är korrekt, som visas nedan!

Python-funktion för att visa Pascals triangel för antal rader ≤ 5

Båda metoderna vi har gått igenom fungerar bra för att visa Pascals triangel för ett godtyckligt antal rader ’numRows’.

Det finns dock tillfällen då vi bara behöver visa Pascals triangel för ett mindre antal rader. Om antalet rader inte överstiger 5 kan vi använda en enkel teknik.

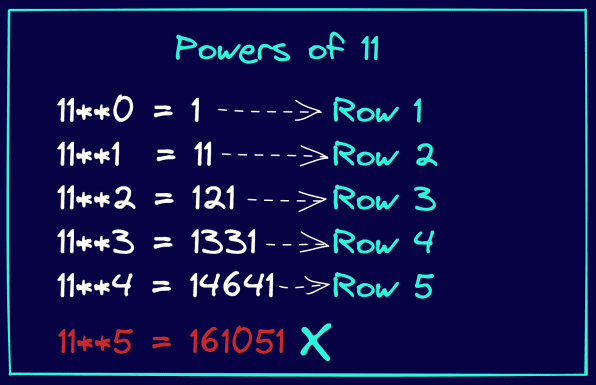
Titta på figuren nedan. Lägg märke till hur potenserna av 11 är identiska med elementen i Pascals triangel. Detta fungerar endast upp till fjärde potensen av 11. Det vill säga 11 upphöjt till {0, 1, 2, 3, 4} ger elementen i raderna 1 till 5 i Pascals triangel.

Låt oss skriva om funktionsdefinitionen som visas nedan:

def pascal_tri(numRows):
  '''Visar Pascals triangel med numRows.'''
  for i in range(numRows):
    print(' '*(numRows-i-1), end='')
    # Beräkna potens av 11
    print(' '.join(str(11**i)))

Så här fungerar funktionen ’pascal_tri’:

Precis som i de tidigare exemplen justerar vi avståndet.
Vi använder Pythons exponentieringsoperator (**) för att beräkna potenserna av 11.
Eftersom potenserna av 11 är heltal, konverterar vi dem till en sträng med ’str()’. Potenserna av 11 är nu strängar.
Strängar i Python är itererbara, så vi kan gå igenom dem och komma åt ett tecken i taget.
Därefter använder vi metoden ’join()’ med syntaxen: ’.join()’ för att sammanfoga elementen i ’’ med ’’ som separator.
Här behöver vi ett enkelt mellanslag mellan tecknen, så ’’ blir ’ ’, och ’’ är strängen som motsvarar en potens av 11.

Låt oss kontrollera att funktionen fungerar som den ska.

pascal_tri(5)

# Utdata
     1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

Som ett annat exempel, anropa funktionen ’pascal_tri’ med 4 som argument.

pascal_tri(4)

# Utdata
     1
    1 1
   1 2 1
  1 3 3 1

Jag hoppas att du nu förstår hur du enkelt kan visa Pascals triangel för ’numRows’ i intervallet 1 till 5.

Slutsats

Här är vad vi har lärt oss:

Hur man konstruerar Pascals triangel med ett givet antal rader. Varje tal i en rad är summan av de två talen direkt ovanför det.
Skapa en Python-funktion med formeln nCr = n!/(n-r)!.r! för att beräkna elementen i Pascals triangel.
Vi har lärt oss en rekursiv implementering av funktionen.
Till sist har vi lärt oss den mest effektiva metoden för att skapa Pascals triangel för upp till 5 rader, genom att använda potenser av 11.

Om du vill förbättra dina Python-kunskaper kan du lära dig att multiplicera matriser, kontrollera om ett tal är ett primtal och lösa problem med strängoperationer. Lycka till med kodningen!