Denna handledning kommer att lära dig hur du skriver ett Python-program för att kontrollera om ett tal är primtal eller inte.
Om du någonsin har tagit upp kodningstest, har du stött på matematikfrågan på provet för primalitet eller för att kontrollera om ett tal är primtal. Och under de närmaste minuterna kommer du att lära dig att komma på den optimala lösningen på denna fråga.
I den här handledningen ska du:
- gå igenom grunderna för primtal,
- skriv Python-kod för att kontrollera om ett tal är primtal, och
- optimera den ytterligare för att få en O(√n) körtidsalgoritm.
För allt detta och mer, låt oss börja.
Innehållsförteckning
Vad är ett primtal?
Låt oss börja med att se över grunderna för primtal.
I talteorin sägs ett naturligt tal n vara främsta om det har exakt två faktorer: 1 och själva talet (n). Kom ihåg från din skolmatte: ett tal i sägs vara en faktor av talet n, om i delar n jämnt. ✅
Följande tabell listar några siffror, alla deras faktorer och om de är primtal.
nFactorsIs Prime?11Nej21, 2Ja31, 3Ja41, 2, 4Nej71, 7Ja151, 3, 5, 15Nej
Från tabellen ovan kan vi skriva ner följande:
- 2 är det minsta primtalet.
- 1 är en faktor för varje tal.
- Varje tal n är en faktor i sig själv.
Så 1 och n är triviala faktorer för vilket tal n som helst. Och ett primtal bör inte ha några andra faktorer än dessa två.
Det betyder att när man går från 2 till n – 1 ska man inte kunna hitta en icke-trivial faktor som delar n utan rest.
O(n) Algoritm för att kontrollera om ett tal är primtal i Python
I det här avsnittet, låt oss formalisera ovanstående tillvägagångssätt till en Python-funktion.
Du kan gå igenom alla tal från 2 till n – 1 med hjälp av objektet range() i Python.
I Python returnerar range(start, stop, step) ett rangeobjekt. Du kan sedan iterera över intervallobjektet för att få en sekvens från start hela vägen upp till stopp -1 i steg i steg.
Eftersom vi behöver mängden heltal från 2 till n-1, kan vi specificera range(2, n) och använda det tillsammans med for loop.
Här är vad vi skulle vilja göra:
- Om du hittar ett tal som delar n jämnt utan en rest, kan du direkt dra slutsatsen att talet inte är primtal.
- Om du har gått igenom hela intervallet av tal från 2 hela vägen upp till n – 1 utan att hitta ett tal som delar n jämnt, då är talet primtal.
Python-funktion för att kontrollera primtal
Med hjälp av ovanstående kan vi gå vidare och definiera funktionen is_prime() enligt följande.
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
Låt oss nu analysera funktionsdefinitionen ovan.
- Ovanstående funktion is_prime() tar in ett positivt heltal n som argument.
- Om du hittar en faktor inom det angivna intervallet (2, n-1) returnerar funktionen False – eftersom talet inte är primtal.
- Och det returnerar True om du korsar hela slingan utan att hitta en faktor.
Låt oss sedan anropa funktionen med argument och verifiera om utdata är korrekt.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True
I utgången ovan ser du att 2 och 11 är primtal (funktionen returnerar True). Och 8 och 9 är inte primtal (funktionen returnerar False).
Hur man optimerar Python-funktionen is_prime()
Vi kan göra en liten optimering här. Observera listan över faktorer i tabellen nedan.
NumberFactors61, 2, 3, 6101, 2, 5, 10181, 2, 3, 6, 9, 18
Tja, vi kan se att den enda faktorn för n som är större än n/2 är n själv.
Så det betyder att du inte behöver loopa hela vägen upp till n – 1. Du kan istället köra loopen bara upp till n/2.
Om du inte hittar en icke-trivial faktor förrän n/2, kan du inte hitta en bortom n/2 heller.
Låt oss nu modifiera funktionen is_prime() för att leta efter faktorer i intervallet (2, n/2)
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return True
Låt oss gå vidare och verifiera resultatet genom några funktionsanrop.
is_prime(9) # False is_prime(11) # True
Även om det kan tyckas som om vi har optimerat, är den här algoritmen inte mer effektiv än den tidigare när det gäller runtime-komplexitet. Faktum är att båda har O(n) runtime-komplexitet: proportionell mot värdet på n eller linjär i n.
Kan vi göra bättre? Ja det kan vi!
▶️ Fortsätt till nästa avsnitt för att avgöra hur du kan förbättra tidskomplexiteten för primtalstestning.
O(√n) Algoritm för att kontrollera primtal i Python
Det händer att faktorerna för ett tal förekommer i par.
Om a är en faktor av talet n, så finns det också en faktor b så att axb = n, eller helt enkelt ab = n.
Låt oss verifiera detta genom ett exempel.
Tabellen nedan visar faktorerna för att talet 18 förekommer i par. Du kan verifiera detsamma för några fler nummer om du vill.
Observera också att √18 är ungefär 4,24.
Och i faktorerna som förekommer i par (a, b) kan du se att om a är mindre än 4,24 så är b större än 4,24 – i det här exemplet (2, 18) och (3, 6).
Faktorer på 18 i par
Figuren nedan visar faktorerna 18 plottade på tallinjen.
Om talet n råkar vara en perfekt kvadrat, har du a = b = √n som en av faktorerna.
▶️ Titta på faktorerna 36 i tabellen nedan. Eftersom 36 är en perfekt kvadrat är a = b = 6 en av faktorerna. För alla andra faktorpar (a, b) gäller a < 6 och b > 6.
Faktorer på 36 i par
Sammanfattningsvis har vi följande:
- Varje tal n kan skrivas som n = axb
- Om n är en perfekt kvadrat, då är a = b = √n.
- Och om a < b, då, a < √n och b > √n.
- Annars, om a > b, då a > √n och b < √n.
Så istället för att gå igenom alla heltal upp till n/2 kan du välja att köra upp till √n. Och detta är mycket effektivare än vårt tidigare tillvägagångssätt.
Hur man ändrar algoritmen is_prime() till O(√n).
Låt oss fortsätta med att optimera funktionen för att leta efter primtal i Python.
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return True
Låt oss nu analysera funktionsdefinitionen ovan:
- För att beräkna kvadratroten ur ett tal, låt oss importera Pythons inbyggda matematikmodul och använda math.sqrt()-funktionen.
- Eftersom n kanske inte är en perfekt kvadrat, måste vi gjuta den till ett heltal. Använd int(var) för att kasta var till en int.
- För att vara säker på att vi faktiskt kontrollerar upp till √n lägger vi till ett plus ett eftersom range()-funktionen exkluderar intervallets slutpunkt som standard.
Kodcellen nedan verifierar att vår funktion is_prime() fungerar korrekt.
is_prime(8) # False is_prime(15) # False is_prime(23) # True
I nästa avsnitt, låt oss skapa några enkla plotter för att förstå O(n) och O(√n) visuellt.
Jämföra O(n) och O(√n) visuellt
▶️ Kör följande kodavsnitt i en Jupyter notebook-miljö som du väljer.
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
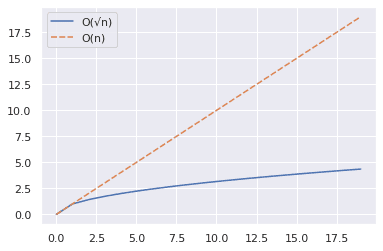
Ovanstående utdrag visar hur du kan rita kurvorna för n och √n för ett värdeintervall.
- Vi använder funktionen NumPy arange() för att skapa en matris med tal.
- Och sedan samlar vi in värdena för n och √n upp till, men inte inklusive 20, till en pandas DataFrame.
- Därefter ritar vi med hjälp av seaborns linjediagram() fungera.
Från diagrammet nedan ser vi att √n är betydligt mindre än n.
Låt oss nu öka intervallet till så högt som 2000 och upprepa samma steg som ovan.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
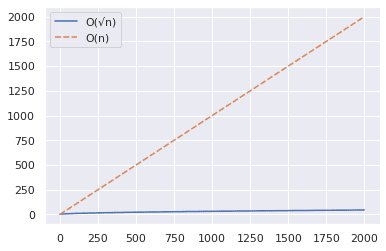
Från ovanstående plot kan du dra slutsatsen att O(√n)-algoritmen är betydligt snabbare när du testar om ett stort tal är primtal.
Här är ett snabbt exempel: 2377 är ett primtal – verifiera detta!😀
Även om O(n)-metoden kommer att ta storleksordningen 2000 steg, kan O(√n)-algoritmen hjälpa till att komma fram till svaret i bara 49 steg.✅
Slutsats
⏳ Och det är dags för en snabb sammanfattning.
- För att kontrollera om ett tal är primtal är den naiva metoden att gå igenom alla tal i intervallet (2, n-1). Om du inte hittar en faktor som delar n, så är n primtal.
- Eftersom den enda faktorn på n större än n/2 är n själv, kan du välja att bara köra upp till n/2.
- Båda ovanstående tillvägagångssätt har en tidskomplexitet på O(n).
- Eftersom faktorer av ett tal förekommer i par kan du bara köra upp till √n. Denna algoritm är mycket snabbare än O(n). Och vinsten är märkbar när man kontrollerar om ett stort tal är primtal eller inte.
Jag hoppas att du förstår hur man kontrollerar om ett tal är primtal i Python. Som nästa steg kan du kolla in vår handledning om Python-program om strängoperationer – där du lär dig att kontrollera om strängar är palindromer, anagram och mer.
Vi ses i en annan handledning. Tills dess, glad kodning!👩🏽💻